【题目】如图,在△ABC中,点D、E、F 分别在BC、AB、CA上,且DE∥CA,DF∥BA,则下列三种说法:
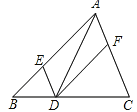
①如果∠BAC=90°,那么四边形AEDF是矩形;
②如果AD平分∠BAC,那么四边形AEDF是菱形;
③如果AD⊥BC 且AB=AC,那么四边形AEDF是菱形。
其中正确的有
A.3个 B.2个 C.1个 D.0个
参考答案:
【答案】A.
【解析】
试题解析:∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形;
∵∠BAC=90°,
∴四边形AEDF是矩形;
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∴∠FAD=∠ADF,
∴AF=DF,
∴四边形AEDF是菱形;
∵AD⊥BC且AB=AC,
∴AD平分∠BAC,
∴四边形AEDF是菱形;
故①②③正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).

解:∵∠BAE+∠AED=180°(已知)
∴ AB ∥ ( )
∴∠BAE= ( 两直线平行,内错角相等 )
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣∠2即∠MAE=
∴ ∥NE( )
∴∠M=∠N( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.

(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在0≤t≤20和20<t≤40时,y关于t的函数关系式:当0≤t≤20,y= ; 当20<t≤40时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD四个顶点的坐标分别是A(1,2),B(3,1),C(5,2),D(3,4).将四边形ABCD先向下平移5个单位,再向左平移6个单位,它的像是四边形A′B′C′D′.

(1)作出四边形A′B′C′D′.
(2)写出四边形A′B′C′D′的顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. 3a2﹣a2=2 B. (2a2)2=2a4 C. a6÷a3=a2 D. a3a2=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(﹣x2+3﹣7x)+(5x﹣7+4x2),其中x=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程,
其中可用公理“两点之间,线段最短”来解释的现象有( )
A. ①② B. ①③ C. ②④ D. ③④
相关试题

