【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).

解:∵∠BAE+∠AED=180°(已知)
∴ AB ∥ ( )
∴∠BAE= ( 两直线平行,内错角相等 )
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣∠2即∠MAE=
∴ ∥NE( )
∴∠M=∠N( )
参考答案:
【答案】CD,同旁内角相等,两直线平行。∠AEC,∠AEC,∠NEA,MA,内错角相等,两直线平行。两直线平行,内错角相等。
【解析】试题分析:由已知易得AB∥CD,则∠BAE=∠AEC,又∠1=∠2,所以∠MAE=∠AEN,则AM∥EN,故∠M=∠N.
试题解析:∵∠BAE+∠AED=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∠BAE=∠AEC(两直线平行,内错角相等)
又∵∠1=∠2,
∴∠BAE-∠1=∠AEC-∠2,
即∠MAE=∠AEN,
∴AM∥EN,(内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法对3.07069取近似值,结果是(精确到十分位)________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3x﹣2>x﹣6的最小整数解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,AB∶BC=1∶2,周长为24 cm,则AB=________ cm,AD=________ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.

(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在0≤t≤20和20<t≤40时,y关于t的函数关系式:当0≤t≤20,y= ; 当20<t≤40时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD四个顶点的坐标分别是A(1,2),B(3,1),C(5,2),D(3,4).将四边形ABCD先向下平移5个单位,再向左平移6个单位,它的像是四边形A′B′C′D′.

(1)作出四边形A′B′C′D′.
(2)写出四边形A′B′C′D′的顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F 分别在BC、AB、CA上,且DE∥CA,DF∥BA,则下列三种说法:
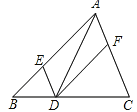
①如果∠BAC=90°,那么四边形AEDF是矩形;
②如果AD平分∠BAC,那么四边形AEDF是菱形;
③如果AD⊥BC 且AB=AC,那么四边形AEDF是菱形。
其中正确的有
A.3个 B.2个 C.1个 D.0个
相关试题

