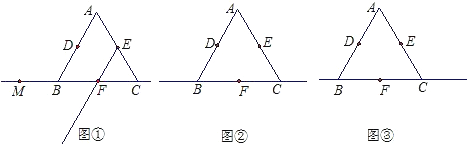
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
参考答案:
【答案】(1)图详见解析,△DMN是等边三角形;(2)△DMN仍是等边三角形,证明详见解析;(3)△DMN不是等边三角形.
【解析】
(1)连接DF,根据等边三角形的性质与三角形中位线平行于第三边并且等于第三边的一半的性质可以证明DF=BD=EF=BF,然后证明BM=FN,∠MBD=∠NFD=120°,从而证明△BDM与△FDN全等,根据全等三角形对应边相等可得MD=DN,对应角相等可得∠MDB=∠NDF,然后证明∠MDN=∠BDF=60°,所以△DMN是等边三角形;(2)连接DF,根据等边三角形的性质与三角形中位线平行于第三边并且等于第三边的一半的性质可以证明DF=BD=EF=BF,然后证明BM=FN,∠MBD=∠NFD=60°,从而证明△BDM与△FDN全等,根据全等三角形对应边相等可得MD=DN,对应角相等可得∠MDB=∠NDF,然后证明∠MDN=∠BDF=60°,所以△DMN是等边三角形; (3)沿用前两问的思路,显然不能证明△CDM与△FDN全等,所以△DMN不是等边三角形.
解:(1)如图①,
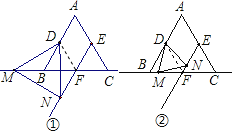
△DMN是等边三角形.
(2)如图②,当M在线段BF上(与点B、F重合)时,△DMN仍是等边三角形.
证明:连接DF,
∵△ABC是等边三角形,
∴∠ABC=60°,AB=AC=BC.
∵D、E、F分别是△ABC三边的中点,
∴DE、DF、EF是等边三角形的中位线.
∴DF=![]() AC,BD=
AC,BD=![]() AB,EF=
AB,EF=![]() AB,BF=
AB,BF=![]() BC.
BC.
∴∠BDF=∠A=∠DFE=60°,DF=BF=EF,
∴∠ABC=∠DFE,
∵FM=EN,
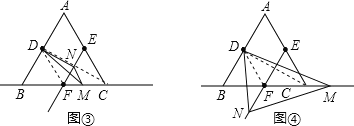
∴BM=NF,
∴△BDM≌△FDN,
∴∠BDM=∠FDN,MD=ND,
∴∠BDM+∠MDF=∠FDN+∠MDF=∠MDN=60°,
△DMN是等边三角形;
(3)如图③或图④,当点M在射线FC上(与点F不重合)时,(1)中的结论不成立,
即△DMN不是等边三角形.
-
科目: 来源: 题型:
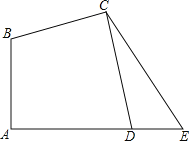
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.连接CE.求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请按要求完成下面三道小题.
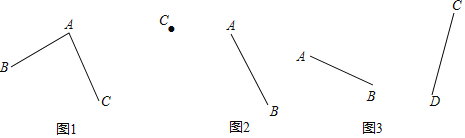
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请画出对称轴a(尺规作图,保留作图痕迹);如果不是,请说明理由.
(2)如图2,已知线段AB和点C.求作线段CD(不要求尺规作图),使它与AB成轴对称,且A与C是对称点,明对称轴b,并简述画图过程.
(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法;如果不能,请说明理由.
-
科目: 来源: 题型:
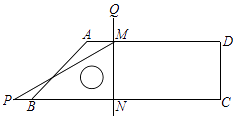
查看答案和解析>>【题目】已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球.
某校羽毛球队需要购买
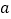 副球拍和
副球拍和 盒羽毛球
盒羽毛球 .
.(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含
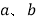 的代数式表示;
的代数式表示;(2)当
 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?(3)当
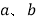 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题
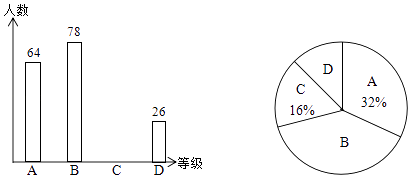
(1)在这次抽样调查中,一共抽取了名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t;5辆大货车与6辆小货车一次可以运货35t
(1)每辆大货车和每辆小货车一次各可以运货多少?
(2)现在租用这两种火车共10辆,要求一次运输货物不低于30t,则大货车至少租几辆?
相关试题

