【题目】已知四边形ABCD,∠ABC=45°,∠C=∠D=90°,含30°角(∠P=30°)的直角三角板PMN(如图)在图中平移,直角边MN⊥BC,顶点M、N分别在边AD、BC上,延长NM到点Q,使QM=PB.若BC=10,CD=3,则当点M从点A平移到点D的过程中,点Q的运动路径长为 . 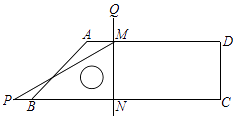
参考答案:
【答案】7
【解析】解:当点M与A重合时,易知PB=3 ![]() ﹣3,当点M与D重合时,易知PB=10﹣3
﹣3,当点M与D重合时,易知PB=10﹣3 ![]() ,
,
∵MQ=PB,
∴点Q的运动路径长=点P的运动路径长=3 ![]() ﹣3+10﹣3
﹣3+10﹣3 ![]() =7,
=7,
所以答案是7.
【考点精析】利用相似三角形的应用对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个内角为60°的菱形的面积是8
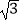 ,则它的内切圆的半径为 .
,则它的内切圆的半径为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.连接CE.求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请按要求完成下面三道小题.
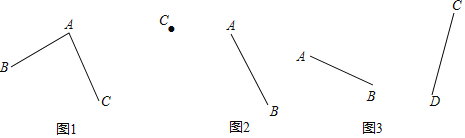
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请画出对称轴a(尺规作图,保留作图痕迹);如果不是,请说明理由.
(2)如图2,已知线段AB和点C.求作线段CD(不要求尺规作图),使它与AB成轴对称,且A与C是对称点,明对称轴b,并简述画图过程.
(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请描述操作方法;如果不能,请说明理由.
-
科目: 来源: 题型:
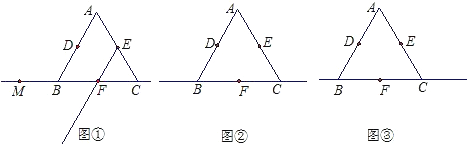
查看答案和解析>>【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商店出售同样牌子和规格的羽毛球拍和羽毛球,每副球拍定价300元,每盒羽毛球定价40元,为庆祝五一节,两家商店开展促销活动如下:
甲商店:所有商品9折优惠;
乙商店:每买1副球拍赠送1盒羽毛球.
某校羽毛球队需要购买
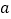 副球拍和
副球拍和 盒羽毛球
盒羽毛球 .
.(1)按上述的促销方式,该校羽毛球队在甲、乙两家商店各应花费多少元?试用含
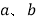 的代数式表示;
的代数式表示;(2)当
 时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?
时,试判断分别到甲、乙两家商店购买球拍和羽毛球,哪家便宜?(3)当
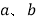 满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同?
满足什么关系时,到甲、乙两家商店购买球拍和羽毛球的费用相同? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题
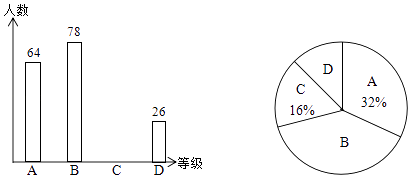
(1)在这次抽样调查中,一共抽取了名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B的人数.
相关试题

