搜索
【题目】如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是_____．
参考答案：
【答案】AC⊥BD
【解析】
根据三角形的中位线定理，可以证明所得四边形的两组对边分别和两条对角线平行，所得四边形的两组对边分别是两条对角线的一半，再根据平行四边形的判定就可证明该四边形是一个平行四边形；所得四边形要成为矩形，则需有一个角是直角，故对角线应满足互相垂直．
解：如图，
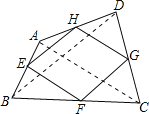
∵E，F分别是边AB，BC的中点，
∴EF∥AC，EF=
AC，
同理HG∥AC，HG=AC，
∴EF∥HG，EF=HG，
∴四边形EFGH是平行四边形；
要使四边形EFGH是矩形，则需EF⊥FG，即AC⊥BD；
故答案为：AC⊥BD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数:y=-10x+500．
（1）李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
（2）设李明获得的利润为W（元）,当销售单价定为多少元时,每月可获得最大利润?
（3）物价部门规定,这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，有一块直角三角形纸片，AC=6，BC=8，现将△ABC沿直线AD折叠，使AC落在斜边AB上，且C与点E重合，则AD的长为________．
-
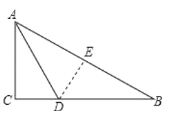
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax
+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①抛物线与x轴的另一个交点是（5，0）；②4a+c＞2b；③4a+b=0；④当x＞-1时，y的值随x值的增大而增大．其中正确的结论有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把一个木制正方体的表面涂上颜色，然后将正方形分割成27个大小相同的小正方体，从这些小正方体中任意取出一个，求取出的小正方体；
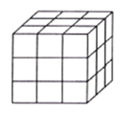
（1）只有一面涂有颜色的概率；
（2）至少有两面涂有颜色的概率；
（3）各个面都没有颜色的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC的顶点A、B、C在边长为1的网格格点上．
（1）画△ABC绕点O逆时针旋转90°得到的△A1B1C1；
（2）画△A1B1C1关于点O的中心对称图形△A2B2C2；
（3）平行四边形A1B1A2B2的面积为______．
-
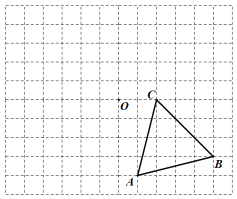
科目： 来源： 题型：
查看答案和解析>>【题目】中华文明，源远流长，中华汉字，寓意深广。为了传承优秀传统文化，某校团委组织了一次全校1500名学生参加的“汉字听写”大赛，为了更好地了解本次大赛的成绩分布情况，随机抽取了部分学生的成绩作为样本进行整理，得到下列不完整的统计图表． 请你根据表中提供的信息，解答下列问题：
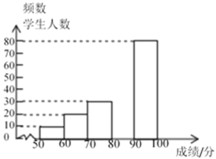
成绩x/分
频数
频率
50≤x＜60
10
0.05
60≤x＜70
20
0.10
70≤x＜80
30
b
80≤x＜90
a
0.30
90≤x≤100
80
0.40
（1）此次调查的样本容量为_____；
（2）在表中：
=_____，
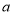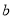=______；（3）补全频数分布直方图；
（4）若成绩在80分以上（包括80分）的为“A”级，则该校参加这次比赛的1500名学生中，成绩为“A”级的约有多少人？
相关试题
