【题目】七年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答下列问题.
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
一班人数/人 | 1 | 1 | 1 | 4 | 0 | 3 |
二班人数/人 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别求一班和二班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表本年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
参考答案:
【答案】(1)一班进球平均数7个,二班进球平均数7个;一班投中众数为7个,二班投中众数为7个;一班中位数为7个,二班中位数为7个.
(2)如果争取夺得总进球数团体第一名,应该选择二班;如果要争取个人进球数进入学校前三名,应该选择一班.
【解析】试题分析:(1)利用平均数、中位数和众数的定义直接求出;
(2)根据方差和个人发挥的最好成绩进行选择.
试题解析:(1)一班进球平均数: ![]() (10×1+9×1+8×1+7×4+6×0+5×3)=7(个),
(10×1+9×1+8×1+7×4+6×0+5×3)=7(个),
二班进球平均数: ![]() (10×0+9×1+8×2+7×5+6×0+5×2)=7(个),
(10×0+9×1+8×2+7×5+6×0+5×2)=7(个),
一班投中7个球的有4人,人数最多,故众数为7(个);
二班投中7个球的有5人,人数最多,故众数为7(个);
一班中位数:第五第六名同学进7个球,故中位数为7(个);
二班中位数:第五第六名同学进7个球,故中位数为7(个).
(2)一班的方差S12=![]() [(10-7)2+(9-7)2+(8-7)2+4×(7-7)2+0×(6-7)2+3×(5-7)2]=2.6,
[(10-7)2+(9-7)2+(8-7)2+4×(7-7)2+0×(6-7)2+3×(5-7)2]=2.6,
二班的方差S22=![]() [0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+(6-7)2+2×(5-7)2]=1.4,
[0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+(6-7)2+2×(5-7)2]=1.4,
二班选手水平发挥更稳定,争取夺得总进球数团体第一名,应该选择二班;
一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度可能是( )
A.第一次右拐15°,第二次左拐165°
B.第一次左拐15°,第二次右拐15°
C.第一次左拐15°,第二次左拐165°
D.第一次右拐15°,第二次右拐15° -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年5月31日,我国飞人苏炳添在美国尤金举行的国际田联钻石联赛100米男子比赛中,获得好成绩,成为历史上首位突破10秒大关的黄种人.如表是苏炳添近五次大赛参赛情况:
比赛日期
2012-8-4
2013-5-21
2014-9-28
2015-5-20
2015-5-31
比赛地点
英国伦敦
中国北京
韩国仁川
中国北京
美国尤金
成绩(秒)
10.19
10.06
10.10
10.06
9.99
则苏炳添这五次比赛成绩的众数和平均数分别为( )
A.10.06秒,10.06秒 B.10.10秒,10.06秒
C.10.06秒,10.08秒 D.10.08秒,10.06秒
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式,错误的是( )
A. (x2y3)2=x4y6B. (﹣xy)3=﹣xy3C. (3m2n2)2=9m4n4D. (﹣a2b3)2=a4b6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列实数是负数的是( )
A. 0.1B. -1C. 1D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个同学对问题“若方程组
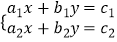 的解是
的解是 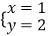 ,求方程组
,求方程组  的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以3,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以3,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣2)2015×(﹣ )2014
)2014
(2)2x3(﹣3x)2÷(﹣x)
(3)(6m2n﹣6m2n2﹣3m2)÷(﹣3m2)
(4)(﹣1)100﹣(3+π)0﹣(﹣ )﹣2 .
)﹣2 .
相关试题

