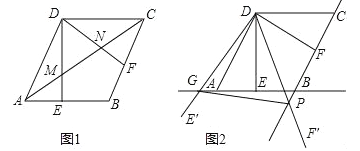
【题目】(2016山东潍坊第24题)如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
参考答案:
【答案】(1)详见解析;(2)将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于3![]() .
.
【解析】
试题分析:(1)连接BD,易证△ABD为等边三角形,由等腰三角形的三线合一得到AE=EB,根据相似三角形的性质解答即可;(2)分∠EDF顺时针旋转和逆时针旋转两种情况,根据旋转变换的性质解答即可.
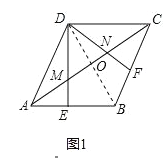
试题解析:(1)证明:如图1,连接BD,交AC于O,
在菱形ABCD中,∠BAD=60°,AD=AB,
∴△ABD为等边三角形,
∵DE⊥AB,
∴AE=EB,
∵AB∥DC,
∴![]() =
=![]() ,
,
同理,![]() =
=![]() ,
,
∴MN=![]() AC;
AC;
(2)解:∵AB∥DC,∠BAD=60°,
∴∠ADC=120°,又∠ADE=∠CDF=30°,
∴∠EDF=60°,
当∠EDF顺时针旋转时,
由旋转的性质可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,
DE=DF=![]() ,∠DEG=∠DFP=90°,
,∠DEG=∠DFP=90°,
在△DEG和△DFP中,
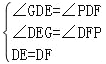 ,
,
∴△DEG≌△DFP,
∴DG=DP,
∴△DGP为等边三角形,
∴△DGP的面积=![]() DG2=3
DG2=3![]() ,
,
解得,DG=2![]() ,
,
则cos∠EDG=![]() =
=![]() ,
,
∴∠EDG=60°,
∴当顺时针旋转60°时,△DGP的面积等于3![]() ,
,
同理可得,当逆时针旋转60°时,△DGP的面积也等于3![]() ,
,
综上所述,将△EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积等于3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.2a2+3a2=a4
B.5a2﹣2a2=3
C.a3×2a2=2a6
D.3a6÷a2=3a4 -
科目: 来源: 题型:
查看答案和解析>>【题目】据某省统计局发布,2017年该省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年该省有效发明专利为a万件,则2018年该省有效发明专利为( )
A. (1+2×22.1%)a B. (1+22.1%)×2a
C. (1+22.1%)2a D. 22.1%×2a
-
科目: 来源: 题型:
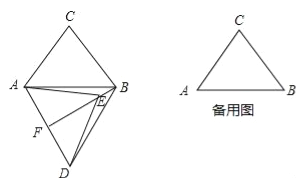
查看答案和解析>>【题目】在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F.
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
③请直接写出BE的长;
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
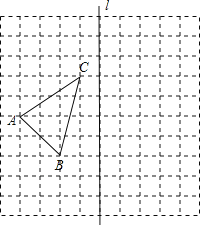
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角板如图甲放置,其中
 ,
,  ,
,  ,斜边
,斜边 ,
,  ,把
,把 绕点
绕点 顺时针旋转
顺时针旋转 得到
得到 (如图乙),这时
(如图乙),这时 与
与 相交于点
相交于点 ,与
,与 相交于点
相交于点 .
.(
 )求
)求 的度数.
的度数.(
 )求线段
)求线段 的长.
的长.(
 )若把
)若把 绕点
绕点 顺时针旋转
顺时针旋转 得到
得到 ,这时点
,这时点 在
在 的内部,外部,还是边上?证明你的判断.
的内部,外部,还是边上?证明你的判断.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个角是70°39′,则它的余角的度数是 .
相关试题

