【题目】如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为 . 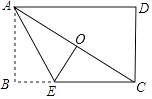
参考答案:
【答案】6
【解析】解:由题意得:AB=AO=CO,即AC=2AB,
且OE垂直平分AC,
∴AE=CE,
设AB=AO=OC=x,
则有AC=2x,∠ACB=30°,
在Rt△ABC中,根据勾股定理得:BC= ![]() x,
x,
在Rt△OEC中,∠OCE=30°,
∴OE= ![]() EC,即BE=
EC,即BE= ![]() EC,
EC,
∵BE=3,
∴OE=3,EC=6,
则AE=6,
所以答案是:6
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF;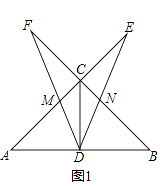
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
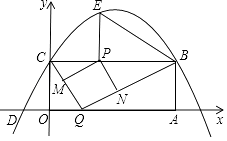
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
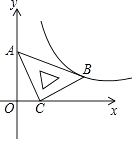
A.( ,0)
,0)
B.(2,0)
C.( ,0)
,0)
D.(3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ;
;
其中正确的是(把你认为正确结论的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣ |﹣
|﹣  +20170;
+20170;
(2)解方程: =
=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E、C、F在一条直线上,AB=DF,AC=DF,BE=FC.

(1)求证:△ABC≌△DFE;
(2)连接AF、BD,求证:四边形ABDF是平行四边形.
相关试题

