【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.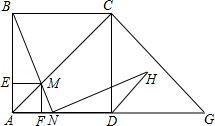
(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.
参考答案:
【答案】
(1)
解:存在;当点M为AC的中点时,AM=BM,则△ABM为等腰三角形;
当点M与点C重合时,AB=BM,则△ABM为等腰三角形;
当点M在AC上,且AM=2时,AM=AB,则△ABM为等腰三角形;
当点M在AC上,且AM=BM时,AM= ![]() AC=
AC= ![]() ×2
×2 ![]() =
= ![]() 时,则△ABM为等腰三角形;
时,则△ABM为等腰三角形;
当点M为CG的中点时,AM=BM,则△ABM为等腰三角形;
(2)
证明:在AB上截取AK=AN,连接KN;如图1所示:

∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∴∠CDG=90°,
∵BK=AB﹣AK,ND=AD﹣AN,
∴BK=DN,
∵DH平分∠CDG,
∴∠CDH=45°,
∴∠NDH=90°+45°=135°,
∴∠BKN=180°﹣∠AKN=135°,
∴∠BKN=∠NDH,
在Rt△ABN中,∠ABN+∠ANB=90°,
又∵BN⊥NH,
即∠BNH=90°,
∴∠ANB+∠DNH=180°﹣∠BNH=90°,
∴∠ABN=∠DNH,
在△BNK和△NHD中,
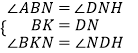 ,
,
∴△BNK≌△NHD(ASA),
∴BN=NH;
(3)
解:①当M在AC上时,即0<t≤2 ![]() 时,△AMF为等腰直角三角形,
时,△AMF为等腰直角三角形,
∵AM=t,
∴AF=FM= ![]() t,
t,
∴S= ![]() AFFM=
AFFM= ![]() ×
× ![]() t×
t× ![]() t=
t= ![]() t2;
t2;
当t=2 ![]() 时,S的最大值=
时,S的最大值= ![]() ×(2
×(2 ![]() )2=2;
)2=2;
②当M在CG上时,即2 ![]() <t<4
<t<4 ![]() 时,如图2所示:
时,如图2所示:
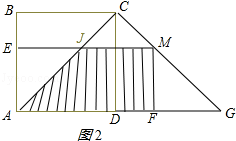
CM=t﹣AC=t﹣2 ![]() ,MG=4
,MG=4 ![]() ﹣t,
﹣t,
在△ACD和△GCD中,
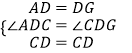 ,
,
∴△ACD≌△GCD(SAS),
∴∠ACD=∠GCD=45°,
∴∠ACM=∠ACD+∠GCD=90°,
∴∠G=90°﹣∠GCD=45°,
∴△MFG为等腰直角三角形,
∴FG=MGcos45°=(4 ![]() ﹣t)
﹣t) ![]() =4﹣
=4﹣ ![]() t,
t,
∴S=S△ACG﹣S△CMJ﹣S△FMG= ![]() ×4×2﹣
×4×2﹣ ![]() ×CM×CM﹣
×CM×CM﹣ ![]() ×FG×FG
×FG×FG
=4﹣ ![]() (t﹣2
(t﹣2 ![]() )2﹣
)2﹣ ![]() (4﹣
(4﹣ ![]() )2=﹣
)2=﹣ ![]() +4
+4 ![]() t﹣8
t﹣8
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,S的最大值为
时,S的最大值为 ![]() .
.
【解析】(1)四种情况:当点M为AC的中点时,AM=BM;当点M与点C重合时,AB=BM;当点M在AC上,且AM=2时,AM=AB;当点M在AC上,且AM=BM时,AM= ![]() 时;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;(3)①当M在AC上时,即0<t≤2
时;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;(3)①当M在AC上时,即0<t≤2 ![]() 时,△AMF为等腰直角三角形,得出AF=FM=
时,△AMF为等腰直角三角形,得出AF=FM= ![]() t,求出S=
t,求出S= ![]() AFFM=
AFFM= ![]() t2;当t=2
t2;当t=2 ![]() 时,即可求出S的最大值;
时,即可求出S的最大值;
②当M在CG上时,即2 ![]() <t<4
<t<4 ![]() 时,先证明△ACD≌△GD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=4﹣
时,先证明△ACD≌△GD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MGcos45°=4﹣ ![]() t,得出S=S△ACG﹣S△CMJ﹣S△FMG , S为t的二次函数,即可求出结果.
t,得出S=S△ACG﹣S△CMJ﹣S△FMG , S为t的二次函数,即可求出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】冠状病毒有多种类型,新型冠状病毒也是其中的一种.冠状病毒的直径在60﹣220纳米之间,平均直径为100纳米左右(1纳米=10﹣9米).那么100纳米可用科学记数法表示为( )
A.100×10﹣9米B.100×109米C.1×10﹣7米D.1×107米
-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营A种品牌的玩具,购进时间的单价是30元,但据市场调查,在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量;
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付他库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多? -
科目: 来源: 题型:
查看答案和解析>>【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;

(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
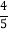 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
相关试题

