【题目】如图①,在长方形ABCD中,AB=10cm,BC=8cm、点P从A出发,沿A、B、C、D路线运动,到D停止;点P的速度为每秒1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,△APD的面积S1(cm2)与x(秒)的函数关系图象;
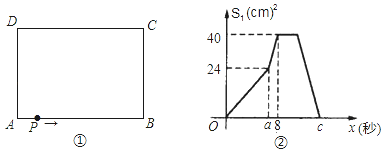
(1)根据图②中提供的信息,求a、b及图②中c的值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的函数关系式;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的![]() ?
?
参考答案:
【答案】(1)a=6,b=2,c=17;(2) y=2x﹣6;(3) 5秒或14.5秒.
【解析】
(1)根据三角形的面积公式可求a、b及图②中c的值;
(2)确定y与x的等量关系后列出关系式即可;
(3)①P在AB上运动时,S△APD=![]() ,AP为运动时间t的一次函数;
,AP为运动时间t的一次函数;
②P在BC上运动时S△APD=![]() 为定值.
为定值.
③P在DC段上运动时,S△APD=![]() .DP为P点运动时间的一次函数.
.DP为P点运动时间的一次函数.
先计算△APD的面积,然后将计算出来的数值代入所求函数的不同分段,解出对应的x的值,若解出的x值在对应的分段区间内,则x的值即为所求的解,反之则不是.
解:(1)根据图象可知S△APD=![]() =
=![]() ×8×(1×a)=24
×8×(1×a)=24
∴a=6
![]() =2
=2
![]() =17
=17
(2)∵a=6,b=2,
∴动点P改变速度后y与出发后的运动时间x(秒)的函数关系式为:y=6+2(x﹣6)=2x﹣6
(3)①当0≤x≤6时
AP=x(cm)
S△APD=![]() =4x
=4x
②当6<x≤8时
AP=6+(x﹣6)×2=2x﹣6
S△APD=![]() =8x﹣24
=8x﹣24
③当x运动到C点时
2x﹣6=18解得:x=12
即:8<x≤12时
S△APD=![]() =40
=40
④当12<x≤17时
DP=2DC+BC﹣(2x﹣6)=﹣2x+34
S△APD=![]() =﹣8x+136
=﹣8x+136
综上:S△APD= ;
;
S△APD=![]() =20
=20
①4x=20时,x=5∈[0,6],符合
②2x﹣6=20时,x=13(6,8],舍去
③8<x≤12时,S△APD=40≠24,舍去
④﹣8x+136=20,x=14.5∈(8,12],符合
所以点P出发后5秒或14.5秒,△APD的面积S1是长方形ABCD面积的![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
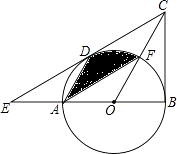
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
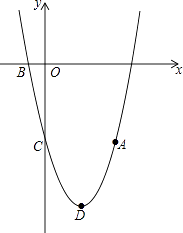
(1)求这条抛物线的表达式;
(2)连结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )

A.
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①
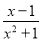 ;②
;②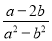 ;③
;③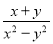 ;④
;④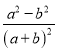 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);(2)若
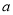 为正整数,且
为正整数,且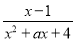 为“和谐分式”,请写出
为“和谐分式”,请写出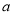 的值;
的值;(3)在化简
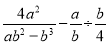 时,
时,小东和小强分别进行了如下三步变形:
小东:
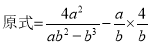
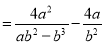

小强:
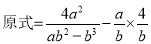
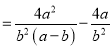
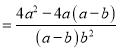
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了
 ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
相关试题

