【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 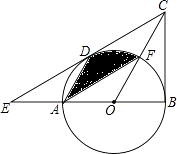
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OD,与AF相交于点G,
∵CE与⊙O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠DOC,∠DAO=∠BOC,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠DOC=∠BOC,
在△CDO和△CBO中,\
 ,
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是⊙O的切线
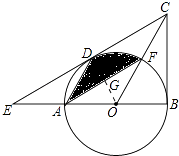
(2)由(1)可知∠DOA=∠BCO,∠DOC=∠BOC,
∵∠ECB=60°,
∴∠DCO=∠BCO= ![]() ∠ECB=30°,
∠ECB=30°,
∴∠DOC=∠BOC=60°,
∴∠DOA=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠GOF=∠ADO,
在△ADG和△FOG中,
 ,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴⊙O的半径r=3,
∴S阴=S扇形ODF= ![]() =
= ![]() π.
π.
【解析】(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.(2)首先证明S阴=S扇形ODF , 然后利用扇形面积公式计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的底边BC=10cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)△ABC的面积S(cm2)与高线h(cm)之间的关系式是什么?
(3)用表格表示当h由4cm变到10cm时(每次增加1cm),S的相应值;
(4)当h每增加1cm时,S如何变化?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题
土特产种类
甲
乙
丙
每辆汽车运载量(吨)
8
6
5
每吨土特产获利(百元)
12
16
10
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
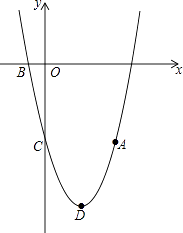
(1)求这条抛物线的表达式;
(2)连结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )

A.
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形ABCD中,AB=10cm,BC=8cm、点P从A出发,沿A、B、C、D路线运动,到D停止;点P的速度为每秒1cm,a秒时点P的速度变为每秒bcm,图②是点P出发x秒后,△APD的面积S1(cm2)与x(秒)的函数关系图象;
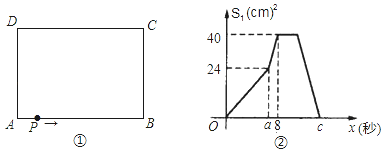
(1)根据图②中提供的信息,求a、b及图②中c的值;
(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的函数关系式;
(3)点P出发后几秒,△APD的面积S1是长方形ABCD面积的
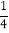 ?
?
相关试题

