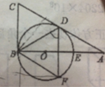
【题目】如图,Rt△ABC中,∠ABC=900,AC=2BC=![]() ,点O在边AB上,以点O为圆心,,OB的长为半径的圆恰好与AC相切于D,与边AB相交于点E.
,点O在边AB上,以点O为圆心,,OB的长为半径的圆恰好与AC相切于D,与边AB相交于点E.
(1)求证:点D为AC的中点;
(2)若点F为半圆BEF上的动点,连接BD、BF、DF,填空:
当∠BDF= 时,四边形BCDF为菱形;
当△BDF为直角三角形时,BF= .
参考答案:
【答案】(1)证明见解析;(2)①60°;②2或1.
【解析】分析:(1)连接OD,只要证明△BCD是等边三角形,△ABD是等腰三角形即可证得结论;
(2)①当DF⊥AB时,四边形BCDF是菱形,因为∠BDC=60°, ∠ADF=60°,可求出∠BOF的度数;
②分别从∠BDF=90°,∠DBF=90°,∠BFD=90°去分析求解,即可求得答案.
详解:![]() ,
,
![]() ,
,
∵BC=CD,
∴△BCD是等边三角形,
∴BC=CD=BD.
如图,连接![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴∠OBD=∠ODB=30°,
∴∠OBD=∠A,
∴BD=AD,
∴CD=AD,
即点D为AC的中点;
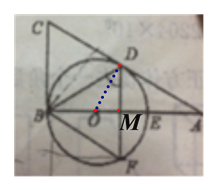
(2)①当DF⊥AB时,四边形BCDF是菱形;
如图,设DF交AB于点M,则DF=2DM,
∵∠A=30°,
∴AD=2DM,
∴DF=AD=BC,
∵∠ABC=90°,
∴DF∥BC,
∴四边形BCDF是平行四边形,
∵BC=CD,
∴四边形BCDF是菱形;
∵∠A=30°,
∴∠ADM=90°-30°=60°,
∴∠BDF=180°-60°-60°=60°,
②若∠BDF=90°,则点E与点F重合,
∵AC=2BC=![]() ,
,
∴BD=![]() ,
,
∴BF=![]() ;
;
若∠DBF=90°,则DF是直径,
∴BF=![]() ;
;
若∠BFD=90°,
∵AD不是直径,
∴∠AED≠90°;
综上可得:当△BDF为直角三角形时,BF等于2或1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,矩形
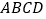 的面积为
的面积为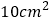 ,它的两条对角线交于点
,它的两条对角线交于点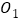 ,以
,以 、
、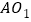 为邻边作平行四边形
为邻边作平行四边形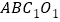 ,平行四边形
,平行四边形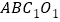 的对角线交于点
的对角线交于点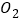 ,同样以
,同样以 、
、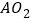 为邻边作平行四边形
为邻边作平行四边形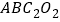 ,……,依次类推,则平行四边形
,……,依次类推,则平行四边形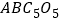 的面积为( )
的面积为( )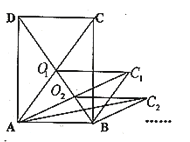
A.
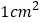 B.
B.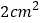 C.
C.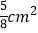 D.
D.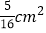
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2
 ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为__________
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
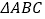 中,点
中,点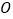 为边
为边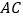 上的一个动点,过点
上的一个动点,过点 作直线
作直线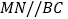 ,设
,设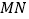 交
交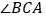 的外角平分线
的外角平分线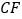 于点
于点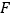 ,交
,交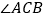 的角平分线
的角平分线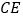 于
于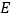 .
.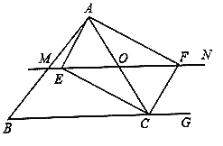
(1)求证:
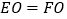 ;
;(2)当点
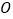 运动到何处时,四边形
运动到何处时,四边形 是矩形?并证明你的结论;
是矩形?并证明你的结论; -
科目: 来源: 题型:
查看答案和解析>>【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔,标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款
在水性笔的质量等因素相同的条件下:
(1)设小明要购买的该品牌笔数是x(x>10)支,则甲商店购买水性笔的费用为 元;乙商店购买水性笔的费用为 元;(用含x的代数式表示,并化简.)
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)当∠A=50°,∠BOD=100°时,判断四边形BECD的形状,并说明理由.

相关试题

