【题目】如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)当∠A=50°,∠BOD=100°时,判断四边形BECD的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形BECD是矩形.
【解析】
(1)由AAS证明△BOE≌△COD,得出OE=OD,即可得出结论;
(2)结论:四边形BECD是矩形.由平行四边形的性质得出∠BCD=∠A=50°,由三角形的外角性质求出∠ODC=∠BCD,得出OC=OD,证出DE=BC,即可得出结论.
(1)证明:∵四边形ABCD为平行四边形,
∴AB∥DC,AB=CD,
∴∠OEB=∠ODC,
又∵O为BC的中点,
∴BO=CO,
在△BOE和△COD中,
 ,
,
∴△BOE≌△COD(AAS);
∴OE=OD,
∴四边形BECD是平行四边形;
(2)解:若∠A=50°,∠BOD=100°时,四边形BECD是矩形.
理由如下:∵四边形ABCD是平行四边形,
∴∠BCD=∠A=50°,
∵∠BOD=∠BCD+∠ODC,
∴∠ODC=100°﹣50°=50°=∠BCD,
∴OC=OD,
∵BO=CO,OD=OE,
∴DE=BC,
∵四边形BECD是平行四边形,
∴四边形BECD是矩形;

-
科目: 来源: 题型:
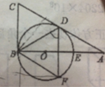
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=900,AC=2BC=
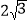 ,点O在边AB上,以点O为圆心,,OB的长为半径的圆恰好与AC相切于D,与边AB相交于点E.
,点O在边AB上,以点O为圆心,,OB的长为半径的圆恰好与AC相切于D,与边AB相交于点E.(1)求证:点D为AC的中点;
(2)若点F为半圆BEF上的动点,连接BD、BF、DF,填空:
当∠BDF= 时,四边形BCDF为菱形;
当△BDF为直角三角形时,BF= .
-
科目: 来源: 题型:
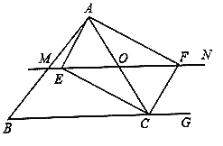
查看答案和解析>>【题目】如图,在
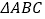 中,点
中,点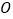 为边
为边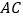 上的一个动点,过点
上的一个动点,过点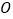 作直线
作直线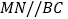 ,设
,设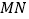 交
交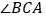 的外角平分线
的外角平分线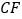 于点
于点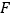 ,交
,交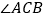 的角平分线
的角平分线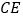 于
于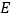 .
.
(1)求证:
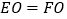 ;
;(2)当点
 运动到何处时,四边形
运动到何处时,四边形 是矩形?并证明你的结论;
是矩形?并证明你的结论; -
科目: 来源: 题型:
查看答案和解析>>【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔,标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款
在水性笔的质量等因素相同的条件下:
(1)设小明要购买的该品牌笔数是x(x>10)支,则甲商店购买水性笔的费用为 元;乙商店购买水性笔的费用为 元;(用含x的代数式表示,并化简.)
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,
 ≈1.732,
≈1.732, ≈1.414)
≈1.414)
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为
 ,并说明理由.
,并说明理由.
相关试题

