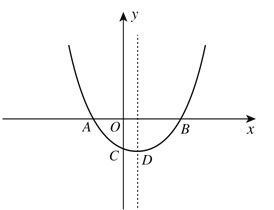
【题目】如图,抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3) 点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似,若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,D(
,D(![]() ,
,![]() );(2)P(
);(2)P(![]() ,
,![]() );(3)存在.N(
);(3)存在.N(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式;
(2)确定出当△ACP的周长最小时,点P就是BC和对称轴的交点,利用两点间的距离公式计算即可;
(3)作出辅助线,利用tan∠MDN=2或![]() ,建立关于点N的横坐标的方程,求出即可.
,建立关于点N的横坐标的方程,求出即可.
试题解析:(1)由于抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,因此把A、B两点的坐标代入
(a≠0)经过A(-1,0),B(2,0)两点,因此把A、B两点的坐标代入![]() (a≠0),可得:
(a≠0),可得:![]() ;解方程组可得:
;解方程组可得: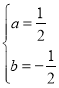 ,故抛物线的解析式为:
,故抛物线的解析式为:![]() ,∵
,∵![]() =
=![]() ,所以D的坐标为(
,所以D的坐标为(![]() ,
,![]() ).
).
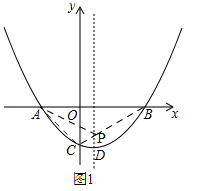
(2)如图1,设P(![]() ,k),∵
,k),∵![]() ,∴C(0,-1),∵A(-1,0),B(2,0),∴A、B两点关于对称轴对称,连接CB交对称轴于点P,则△ACP的周长最小.设直线BC为y=kx+b,则:
,∴C(0,-1),∵A(-1,0),B(2,0),∴A、B两点关于对称轴对称,连接CB交对称轴于点P,则△ACP的周长最小.设直线BC为y=kx+b,则:![]() ,解得:
,解得: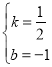 ,∴直线BC为:
,∴直线BC为:![]() .当x=
.当x=![]() 时,
时,![]() =
=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
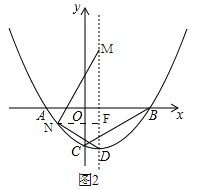
(3)存在.如图2,过点作NF⊥DM,∵B(2,0),C(0,﹣1),∴OB=2,OC=1,∴tan∠OBC=![]() ,tan∠OCB=
,tan∠OCB=![]() =2,设点N(m,
=2,设点N(m,![]() ),∴FN=|m﹣
),∴FN=|m﹣![]() |,FD=|
|,FD=|![]() |=|
|=|![]() |,∵Rt△DNM与Rt△BOC相似,∴∠MDN=∠OBC,或∠MDN=∠OCB;
|,∵Rt△DNM与Rt△BOC相似,∴∠MDN=∠OBC,或∠MDN=∠OCB;
①当∠MDN=∠OBC时,∴tan∠MDN=![]() =
=![]() ,∴
,∴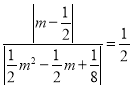 ,∴m=
,∴m=![]() (舍)或m=
(舍)或m=![]() 或m=
或m=![]() ,∴N(
,∴N(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
②当∠MDN=∠OCB时,∴tan∠MDN=![]() =2,∴
=2,∴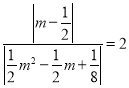 ,∴m=
,∴m=![]() (舍)或m=
(舍)或m=![]() 或m=
或m=![]() ,∴N(
,∴N(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
∴符合条件的点N的坐标(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
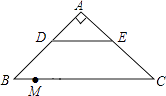
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式的变形正确的是( )
A.若am>bm,则a>b
B.若am2>bm2 , 则a>b
C.若a>b,则am2>bm2
D.若a>b且ab>0,则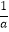 >
> 
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:
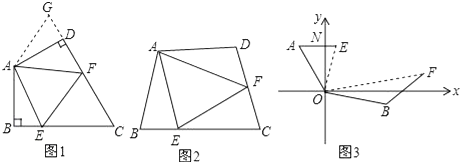
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某钢厂去年一月份某种钢的产量为5000吨,三月份上升到7200吨,这两个月平均每月增长的百分率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=2,则代数式a2b+ab2的值为__________.
相关试题

