Question

【题目】如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为的中点．

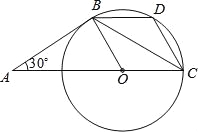
（1）求证：AB=BC；

（2）求证：四边形BOCD是菱形．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】

试题分析：（1）由AB是⊙O的切线，∠A=30°，易求得∠OCB的度数，继而可得∠A=∠OCB=30°，又由等角对等边，证得AB=BC；

（2）首先连接OD，易证得△BOD与△COD是等边三角形，可得OB=BD=OC=CD，即可证得四边形BOCD是菱形．

试题解析：（1）∵AB是⊙O的切线，

∴OB⊥AB，

∵∠A=30°，

∴∠AOB=60°，

∵OB=OC，

∴∠OCB=∠OBC=∠AOB=30°，

∴∠A=∠OCB，

∴AB=BC；

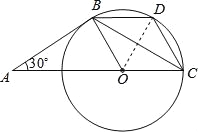
（2）连接OD，

∵∠AOB=60°，

∴∠BOC=120°，

∵D为的中点，

∴，∠BOD=∠COD=60°，

∵OB=OD=OC，

∴△BOD与△COD是等边三角形，

∴OB=BD=OC=CD，

∴四边形BOCD是菱形．