搜索
【题目】如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE＝5
cm， 且tan∠EFC＝
，那么矩形ABCD的周长_____________cm．
参考答案：
【答案】36.
【解析】试题分析：∵△AFE和△ADE关于AE对称，∴∠AFE＝∠D＝90°，AF＝AD，EF＝DE.∵tan∠EFC＝
＝
，∴可设EC＝3x，CF＝4x，那么EF＝5x，∴DE＝EF＝5x.∴DC＝DE＋CE＝3x＋5x＝8x.∴AB＝DC＝8x.
∵∠EFC＋∠AFB＝90°, ∠BAF＋∠AFB＝90°,∴∠EFC＝∠BAF.∴tan∠BAF＝tan∠EFC＝，∴
＝.∴AB＝8x,∴BF＝6x.∴BC＝BF＋CF＝10x.∴AD＝10x.在Rt△ADE中，由勾股定理，得AD2＋DE2＝AE2.∴（10x）2＋（5x）2＝（5
）2.解得x＝1.∴AB＝8x＝8,AD＝10x＝10.∴矩形ABCD的周长＝8×2＋10×2＝36.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司今年销售一种产品，1月份获得利润20万元，由于产品畅销，利润逐月增加，3月份的利润比2月份的利润增加4.8万元，假设该产品利润每月的增长率相同，求这个增长率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为
，把△ABO缩小，则点A的对应点A′的坐标是（ ）
A．（―1，2）
B．（―9，18）
C．（―9，18）或（9，―18）
D．（―1，2）或（1，―2）
-
科目： 来源： 题型：
查看答案和解析>>【题目】用长分别为3cm，4cm，5cm的三条线段可以围成直角三角形的事件是（ ）
A. 必然事件 B. 不可能事件 C. 随机事件 D. 以上都不是
-
科目： 来源： 题型：
查看答案和解析>>【题目】在求1＋3＋32＋33＋34＋35＋36＋37＋38的值时，张红发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S＝1＋3＋32＋33＋34＋35＋36＋37＋38 ①，然后在①式的两边都乘以3，得：3S＝3＋32＋33＋34＋35＋36＋37＋38＋39 ②，
②一①得：3S―S＝39－1，即2S＝39－1，
∴S＝
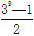.得出答案后，爱动脑筋的张红想：如果把“3”换成字母m（m≠0且m≠1），能否求出1＋m＋m2＋m3＋m4＋…＋m2016的值？如能求出，其正确答案是___________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有四个数：84,76，X，90，它们的平均数为80，则X为（ ）
A. 70 B. 71 C. 72 D. 73
-
科目： 来源： 题型：
查看答案和解析>>【题目】（12分）沿海某市企业计划投入800万元购进A、B两种小型海水淡化设备，这两种设备每台的购入价、每台设备每天可淡化的海水量及淡化率如下表：
每台购入价（万元）
每台每天可淡化海水量（立方米）
淡化率
A型
20
250
80%
B型
25
400
75%
（1）若该企业每天能生产9000立方米的淡化水，求购进A型、B型设备各几台？
（2）在（1）的条件下，已知每淡化1立方米海水所需的费用为1.5元，政府补贴0.3元．企业将淡化水以3.2元/立方米的价格出售，每年还需各项支出61万元．按每年实际生产300天计算，该企业至少几年后能收回成本（结果精确到个位）？
相关试题
