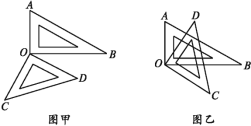
【题目】(1)将一副三角板按图甲的位置放置,那么∠AOD和∠BOC相等吗?∠AOC和∠BOD在数量上有何关系?说明理由.
(2)若将这副三角板按图乙所示摆放,三角板的直角顶点重合在点O处.上述关系还成立吗?
参考答案:
【答案】(1)∠AOD和∠BOC相等,∠AOC和∠BOD互补.理由见解析;(2)成立.理由见解析.
【解析】
(1)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时加上∠BOD可得∠AOD=∠COB;根据周角为360°且∠AOB=∠COD=90°,则∠AOC+∠BOD=360°90°90°=180°可得∠AOC和∠BOD互补;
(2)根据直角三角板可得:∠AOB=∠COD=90°,再根据等式的性质两边同时减去∠BOD可得∠AOD=∠COB;根据角的和差关系可得∠BOD+∠AOC=∠BOD+∠AOB+∠COB=90°+90°=180°,进而可得∠BOD+∠AOC=180°
(1)∠AOD和∠BOC相等,∠AOC和∠BOD互补.
理由:
∵∠AOB=∠COD=90°,
∴∠AOB+∠BOD=∠COD+∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=360°-90°-90°=180°,
∴∠AOC和∠BOD互补.
(2)成立.
理由:
∵∠AOB=∠COD=90°,
∴∠AOB-∠BOD=∠COD-∠BOD,
∴∠AOD=∠COB;
∵∠AOB=∠COD=90°,
∴∠BOD+∠AOC=∠BOD+∠AOB+∠COB=90°+∠BOD+∠COB=90°+∠DOC=90°+90°=180°.
-
科目: 来源: 题型:
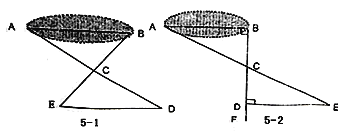
查看答案和解析>>【题目】八(1)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如图5-1,先在平地上取一个可直接到达A、B的点C,连接AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如图5-2,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
阅读后1回答下列问题:
(1)方案(Ⅰ)是否可行?说明理由.
(2)方案(Ⅱ)是否可行?说明理由.
(3)方案(Ⅱ)中作BF⊥AB,ED⊥BF的目的是 ;若仅满足∠ABD=∠BDE≠90°, 方案(Ⅱ)是否成立? .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8.则(62,55)表示的数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小华用除了正面的数字不同其他完全相同的4张卡片玩游戏,卡片上的数字分别是2、4、5、6,他俩将卡片洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的卡片不放回
(1)若小明恰好抽到了标注4的卡片,直接写出小华抽出的卡片上的数字比4大的概率是多少;
(2)小明、小华约定,若小明抽到的卡片的标注数字比小华的大,则小明胜:反之,则小明负,你认为这个游戏是否公平?请用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(1)
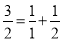 ;
; (2)
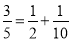 ;
; (3)
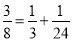 ;
; (4)
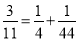 ;
; ……
根据上述等式的规律,解答下列问题:
(1)写出第5个等式:________________;
(2)写出第
 个等式:__________________(用含有
个等式:__________________(用含有 的代数式表示);
的代数式表示);(3)应用你发现的规律,计算:
 。
。
相关试题

