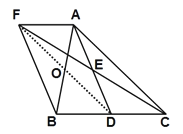
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作AF//BC,交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由.
(2)连接FD,与AB相交于点O,若BO=![]() AC,试判断四边形AFBD的形状,并证明你的结论.
AC,试判断四边形AFBD的形状,并证明你的结论.
参考答案:
【答案】(1)BD=CD,理由见解析;(2)四边形AFBD是矩形,证明见解析.
【解析】
(1)先证明△AFE≌△DCE,从而得到AF=CD,因为AF=BD,则结论得证;
(2)先证明四边形AFBD是平行四边形,再等腰三角形的利用三线合一证得AD⊥BC,即∠ADB=90,即可证得四边形AFBD是矩形.
(1)BD=CD,理由为:
∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=ED,
又∠AEF=∠DEC,
∴△AFE≌△DCE,
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)四边形AFBD是矩形.理由为:
∵AF∥BC,AF=BD,
∴四边形AFBD是平行四边形,
∴BO=![]() AB,
AB,
∵BO=![]() AC
AC
∴ AB=AC,
∵BD=CD,
∴AD⊥BC,即∠ADB=90,
∴四边形AFBD是矩形.
-
科目: 来源: 题型:
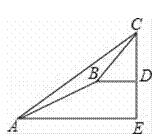
查看答案和解析>>【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车收费标准:3 km以内(含3 km)起步价为8元,超过3 km后每1 km加收1.8元.
(1)若小明坐出租车行驶了6 km,则他应付多少元车费?
(2)如果用s表示出租车行驶的路程,m表示出租车应收的车费,请你表示出s与m之间的数量关系(s>3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的个数是( )
①两点之间的所有连线中,线段最短;②相等的角是对顶角;③过一点有且仅有一条直线与己知直线平行;④两点之间的距离是两点间的线段;⑤若
 ,则点
,则点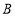 为线段
为线段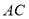 的中点;⑥不相交的两条直线叫做平行线。
的中点;⑥不相交的两条直线叫做平行线。A.
 个B.
个B. 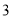 个C.
个C. 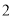 个D.
个D. 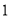 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=
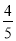 ,求
,求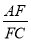 的值.
的值.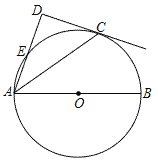
-
科目: 来源: 题型:
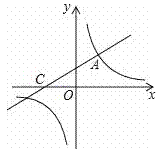
查看答案和解析>>【题目】如图,直线
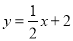 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C. (1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
相关试题

