【题目】如图,以三角形ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC. 
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF= ![]() ,求⊙O的半径r.
,求⊙O的半径r.
参考答案:
【答案】
(1)证明:连接OA、OD,

∵D为弧BE的中点,
∴OD⊥BC,
∠DOF=90°,
∴∠D+∠OFD=90°,
∵AC=FC,OA=OD,
∴∠CAF=∠CFA,∠OAD=∠D,
∵∠CFA=∠OFD,
∴∠OAD+∠CAF=90°,
∴OA⊥AC,
∵OA为半径,
∴AC是⊙O切线;
(2)解:∵⊙O半径是r,
∴OD=r,OF=8-r,
在Rt△DOF中,r2+(8-r)2=( ![]() )2,
)2,
r=6,r=2(舍),
当r=2时,OB=OE=2,OF=BF-OB=8-2=6>OE,
∴r=2舍去;
即⊙O的半径r为6.
【解析】(1)连接OA、OD,求出∠D+∠OFD=90°,推出∠CAF=∠CFA,∠OAD=∠D,求出∠OAD+∠CAF=90°,根据切线的判定推出即可;(2)OD=r,OF=8-r,在Rt△DOF中根据勾股定理得出方程r2+(8-r)2=( ![]() )2 , 求出即可.
)2 , 求出即可.
【考点精析】根据题目的已知条件,利用切线的判定定理的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行收费标准如下:

春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动? -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的集合中.
—7 , 0,
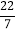 ,—22
,—22 , -2.55555…, 3.01, +9 ,4.020020002…,+10﹪, -2
, -2.55555…, 3.01, +9 ,4.020020002…,+10﹪, -2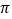 .
.无理数集合:{ }; 负有理数集合:{ };
正分数集合:{ }; 非负整数集合:{ };
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1).
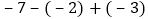 . (2).
. (2).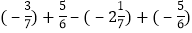
(3).
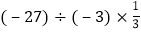 (4).
(4). 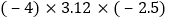
(5).
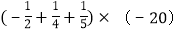 (6).
(6).
(7).
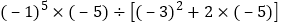 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺如图拼接:含
 角的三角尺
角的三角尺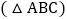 的长直角边与含
的长直角边与含 角的三角尺
角的三角尺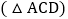 的斜边恰好重合
的斜边恰好重合 已知
已知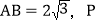 是AC上的一个动点.
是AC上的一个动点.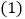 当点P运动到
当点P运动到 的平分线上时,连接DP,求DP的长;
的平分线上时,连接DP,求DP的长;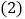 当点P在运动过程中出现
当点P在运动过程中出现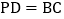 时,求此时
时,求此时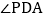 的度数;
的度数; 当点P运动到什么位置时,以
当点P运动到什么位置时,以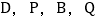 为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.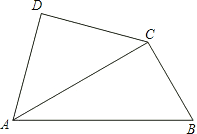
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知12箱苹果,以每箱10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,称重记录如下:
+0.2 ,—0.2,+0. 7,—0.3,—0.4,+0.6,0,—0.1,—0.6,+0.5,—0.2,—0.5。
⑴求12箱苹果的总重量;
⑵若每箱苹果的重量标准为10
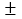 0.5(千克),则这12箱有几箱不合乎标准的?
0.5(千克),则这12箱有几箱不合乎标准的?
相关试题

