【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
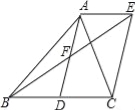
(1)求证:四边形ADCE是平行四边形;
(2)当AB、AC之间满足 时,四边形ADCE是矩形;
(3)当AB、AC之间满足 时,四边形ADCE是正方形.
参考答案:
【答案】(1)证明见解析(2)当AB=AC时(3)当AB=AC,AB⊥AC时
【解析】
试题分析:(1)首先证明△AFE≌△DFB可得AE=BD,进而可证明AE=CD,再由AE∥BC可利用一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;
(2)当AB=AC时,根据等腰三角形三线合一可得AD⊥BC,再根据有一个角是直角的平行四边形是矩形可得结论;
(3)当AB=AC,AB⊥AC时,△ABC是等腰直角三角形,根据直角三角形斜边上的中线等于斜边的一半可得AD=CD,根据等腰三角形的性质可得AD⊥BC,从而可得证明四边形ADCE是正方形.
试题解析: (1)∵AD是△ABC的中线,
∴BD=CD,
∵AE∥BC,
∴∠AEF=∠DBF,
在△AFE和△DFB中,
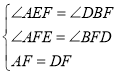 ,
,
∴△AFE≌△DFB(AAS),
∴AE=BD,
∴AE=CD,
∵AE∥BC,
∴四边形ADCE是平行四边形;
(2)当AB=AC时,四边形ADCE是矩形;
∵AB=AC,AD是△ABC的中线,
∴AD⊥BC,
∴∠ADC=90°,
∵四边形ADCE是平行四边形,
∴四边形ADCE是矩形,
故答案为:AB=AC;
(3)当AB⊥AC,AB=AC时,四边形ADCE是正方形,
∵AB⊥AC,AB=AC,
∴△ABC是等腰直角三角形,
∵AD是△ABC的中线,
∴AD=CD,AD⊥BC,
又∵四边形ADCE是平行四边形,
∴四边形ADCE是正方形,
故答案为:AB⊥AC,AB=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照三个内角的大小,可以将三角形分为锐角三角形、、;按照有几条边相等,可以将三角形分为等边三角形、、.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数的混合运算:进行有理数的混合运算时,应注意以下运算顺序:
(1)先________,再________,最后________;
(2)同级运算,从________到________进行;
(3)如有括号,先做括号内的运算,按________括号、________括号、________括号依次进行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62米,到达D点,在测得山顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC(结果精确的1米,参考数值:
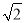 ≈1.4,
≈1.4,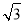 ≈1.7)
≈1.7)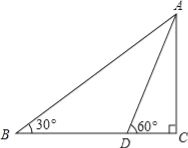
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是常见的安全标记,其中是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
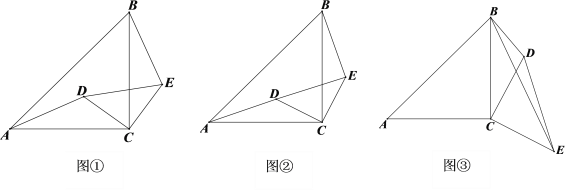
查看答案和解析>>【题目】如图①已知△ACB和△DCE为等腰直角三角形,按如图的位置摆放,直角顶点
C重合.
(1)求证:AD=BE;
(2)将△DCE绕点C旋转得到图②,点A、D、E在同一直线上时,若CD=
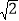 ,BE=3,
,BE=3,求AB 的长;
(3)将△DCE绕点C顺时针旋转得到图③,若∠CBD=45°,AC=6,BD=3,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等、无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的

A.
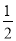 B.
B.  C.
C. 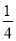 D.
D. 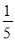
相关试题

