Question

【题目】如图，ABCD为平行四边形，DFEC和BCGH为正方形．求证：AC⊥EG．

Answer 1

【答案】证明：∵四边形BCGH、EFDC为正方形，四边形ABCD为平行四边形， ∴GC∥BH，DC∥AB，∠HBC=∠ECD=90°，
∴∠HBA=∠GCD（两边分别平行的两角相等或互补），
∴∠HBC+∠HBA=∠GCD+∠ECD，即90°+∠HBA=∠GCD+90°，
∴∠GCE=∠ABC，
∴AB=DC=EC，BC=CG，
在△ABC和和△ECG中，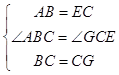
，
∴△ABC≌△ECG（SAS），
∴∠CGE=∠ACB，
∵∠ACB+∠GCA=90°，
∴∠CGE+∠GCA=90°，
∴AC⊥EG．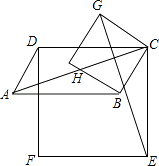

【解析】本题中要证AC⊥EG也就是证∠CGE+∠GCA=90°，我们发现∠GBA+∠ACB=90°，因此证明∠CGE=∠ACB就是问题的关键，我们可通过证明三角形ABC和ECG全等来实现．
【考点精析】本题主要考查了平行四边形的性质和正方形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．