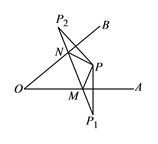
【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
参考答案:
【答案】15 96°
【解析】
P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N.由此即可得到△PMN的周长.根据四边形内角和为360°,可得出∠P1PP2的度数,根据等腰三角形的性质和三角形外角的性质可得出∠PNM+∠PMN的度数,再根据三角形内角和定理即可得出∠MPN的度数.
∵P点关于OA的对称是点P1,P点关于OB的对称点P2,∴PM=P1M,PN=P2N,PP2⊥OB,PP1⊥OA,∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15,∠P1PP2=360°-90°-90°-42°=138°,∠P2=∠NPP2,∠P1=∠P1PM,∴∠PNM=2∠P2,∠PMN=2∠P1,∴∠PNM+∠PMN=2∠P1+2∠P2=2(180°-∠P1PP2)=84°,∴∠MPN=180°-(∠PNM+∠PMN)=180°-84°=96°.
故答案为:15,96°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB、CD外部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明)
(3)如图3,写出∠BPD﹑∠B﹑∠D﹑∠BQD之间的数量关系?请证明你的结论.
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表) 甲超市:
球
两红
一红一白
两白
礼金券(元)
5
10
5
乙超市:
球
两红
一红一白
两白
礼金券(元)
10
5
10
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
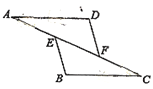
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

-
科目: 来源: 题型:
查看答案和解析>>【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,
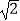 ≈1.414,
≈1.414, 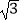 ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 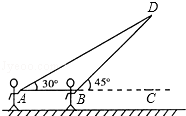
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,3))、B(3,-1),点M在x轴上,当AM-BM最大时,点M的坐标为
A. (2,0) B. (2.5,0) C. (4,0), D. (4.5,0)
相关试题

