Question

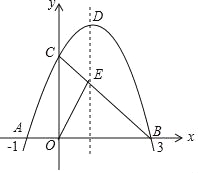
【题目】如图，已知抛物线与轴交于点和点，与轴交于点，连接交抛物线的对称轴于点，是抛物线的顶点．

（1）求此抛物线的解析式；

（2）直接写出点和点的坐标；

（3）若点在第一象限内的抛物线上，且，求点坐标．

注：二次函数（）的顶点坐标为．

Answer 1

【答案】（1）抛物线的解析式为y=﹣x2+2x+3；（2）C（0，3），D（1，4）；（3）P（2，3）．

【解析】

试题分析：（1）将A、B的坐标代入抛物线的解析式中，即可求出待定系数b、c的值，进而可得到抛物线的对称轴方程；

（2）令x=0，可得C点坐标，将函数解析式配方即得抛物线的顶点C的坐标；

（3）设P（x，y）（x＞0，y＞0），根据题意列出方程即可求得y，即得D点坐标．

试题解析：（1）由点A（﹣1，0）和点B（3，0）得 ，解得： ，

∴抛物线的解析式为y=﹣x2+2x+3；

（2）令x=0，则y=3，∴C（0，3），∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴D（1，4）；

（3）设P（x，y）（x＞0，y＞0），S△COE=×1×3=，S△ABP=×4y=2y，

∵S△ABP=4S△COE，∴2y=4×，∴y=3，∴﹣x2+2x+3=3，解得：x1=0（不合题意，舍去），x2=2，

∴P（2，3）．