【题目】已知:如图,在△ABC中,DE、DF是△ABC的中位线,连接EF、AD,其交点为O.求证:

(1)△CDE≌△DBF;
(2)OA=OD.
参考答案:
【答案】见解析.
【解析】
试题分析:根据三角形中位线,可得DF与CE的关系,DB与DC的关系,根据SAS,可得答案;根据三角形的中位线,可得DF与AE的关系,根据平行四边形的判定与性质,可得答案.
试题解析:证明:(1)∵DE、DF是△ABC的中位线,∴DF=CE,DF∥CE,DB=DC.∵DF∥CE,∴∠C=∠BDF.
在△CDE和△DBF中 ,∴△CDE≌△DBF (SAS);
,∴△CDE≌△DBF (SAS);
(2)∵DE、DF是△ABC的中位线,∴DF=AE,DF∥AE,∴四边形DEAF是平行四边形,
∵EF与AD交于O点,∴AO=OD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )

A.
B.
C.
D.10﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
 ,E为AB、CD间的一点,连接EA、EC.
,E为AB、CD间的一点,连接EA、EC. 如图
如图 ,若
,若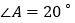 ,
, ,求
,求 的度数;
的度数; 如图
如图 ,若
,若 ,
, ,求
,求 的度数;
的度数;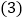 如图
如图 ,若
,若 ,
, ,则
,则 ,
, 与
与 之间有何等量关系
之间有何等量关系 并简要说明.
并简要说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

-
科目: 来源: 题型:
查看答案和解析>>【题目】你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为
 ,瓶中水面的高度为
,瓶中水面的高度为 ,下面能大致表示上面故事情节的图象是( )
,下面能大致表示上面故事情节的图象是( ) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题

(1)公共阅报栏离小红家有______米,小红从家走到公共阅报栏用了______分;
(2)小红在公共阅报栏看新闻一共用了______分;
(3)邮亭离公共阅报栏有______米,小红从公共阅报栏到邮亭用了______分;
(4)小红从邮亭走回家用了______分,平均速度是______米/秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面的图象记录了某地一月份某大的温度随时间变化的情况,请你仔细观察图象回答下面的问题:

(1)在这个问题中,变量分别是______,时间的取值范围是______;
(2)20时的温度是______℃,温度是0℃的时刻是______时,最暖和的时刻是_______时,温度在-3℃以下的持续时间为______小时;
(3)你从图象中还能获得哪些信息?(写出1~2条即可)
答:__________________________________________________.
相关试题

