【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?

已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
参考答案:
【答案】探究一:∠FDC+∠ECD =180°+∠A;探究二:∠DPC=90°+![]() ∠A;探究三:∠PDC==
∠A;探究三:∠PDC==![]() (∠A+∠B);探究四:∠P=
(∠A+∠B);探究四:∠P=![]() (∠A+∠B+∠E+∠F)﹣180°
(∠A+∠B+∠E+∠F)﹣180°
【解析】试题分析:探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (180°﹣∠A),
(180°﹣∠A),
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°﹣![]() (360°﹣∠A﹣∠B),
(360°﹣∠A﹣∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (720°﹣∠A﹣∠B﹣∠E﹣∠F),
(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=![]() (∠A+∠B+∠E+∠F)﹣180°,
(∠A+∠B+∠E+∠F)﹣180°,
即∠P=![]() (∠A+∠B+∠E+∠F)﹣180°.
(∠A+∠B+∠E+∠F)﹣180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两边长分别为2和5,则它的周长等于______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”应先假设:在一个三角形中( )
A. 至多有一个内角大于或等于60° B. 至多有一个内角大于60°
C. 每一个内角小于或等于60° D. 每一个内角大于60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个相似三角形的周长比是4:9,则对应中线的比是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A,某人在岸边的B处测得A在B的北偏东60°的方向上,然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:
 ≈1.732)
≈1.732)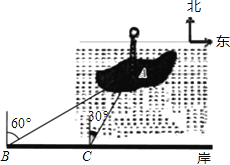
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE。

(1)求证:DC=BE;
(2)试判断∠AFD和∠AFE的大小关系,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数有 ( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系要么相交要么平行;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

