【题目】如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.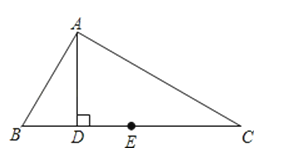
参考答案:
【答案】证明:取AC中点F,连接EF,DF,
则EF为中位线,且EF‖AB、∠FEC=∠B=2∠C,
在直角三角形ACD中,F是斜边AC的中点,
∴DF=CF,
∴∠DEF=∠C,
即有2∠FDC=∠FEC,
∴∠EFC=∠FDC+∠DFE,
∴2∠DFE=∠FEC=2∠FDC,
∴DE=EF,
∴AB=2DE.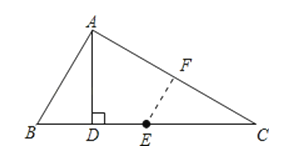
【解析】取AC中点F,连接EF、DF,则EF为△ABC的中位线,结合条件可得到∠FEC=2∠C,结合直角三角形的性质可得到∠EDF=∠EFD,得到DE=EF,可得出结论.
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按括号内的要求,用四舍五入法,对1022.0099取近似值,其中错误的是( )
A.1022.01(精确到0.01)
B.1.0×103(保留2个有效数字)
C.1022(精确到十位)
D.1022.010(精确到千分位) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.两边之和大于第三边B.有一个角的平分线垂直于这个角的对边
C.有两个锐角的和等于90°D.内角和等于180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数
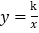 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .
.(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.
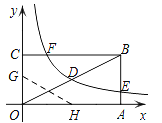
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区有一块长方形的花圃,为了加强对花圃的保护,小区管理人员准备用道砖沿花圃的边缘将其围起来.已知花圃的长是宽的3倍,面积是675平方米.每块道砖的长为50厘米,求一共需要多少块道砖.
-
科目: 来源: 题型:
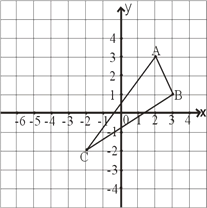
查看答案和解析>>【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直写出D、E、F的坐标.D、E、F点的坐标是:D( , ) E( , ) F( , );
(2)求四边形ABED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经营一种水产品,成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,销售单价定为__________元时,获得的利润最多.
相关试题

