Question

【题目】如图，已知一次函数y=x-3与反比例函数y=的图象相交于点A（4，n），与x轴相交于点B．

（1）填空：n的值为 ，k的值为 ；

（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；

（3）观察反比函数y=的图象，当y≥-2时，请直接写出自变量x的取值范围．

Answer 1

【答案】（1）3，12；（2）D（，3）；（3）或．

【解析】试题分析：（1）把点A（4，n）代入一次函数y=x-3，得到n的值为3；再把点A（4，3）代入反比例函数，得到k的值为12；

（2）根据坐标轴上点的坐标特征可得点B的坐标为（2，0），过点A作AE⊥x轴，垂足为E，过点D作DF⊥x轴，垂足为F，根据勾股定理得到AB=，根据AAS可得△ABE≌△DCF，根据菱形的性质和全等三角形的性质可得点D的坐标；

（3）根据反比函数的性质即可得到当y≥-2时，自变量x的取值范围．

试题解析：（1）把点A（4，n）代入一次函数y=x-3，可得n=×4-3=3；

把点A（4，3）代入反比例函数，可得3=，

解得k=12．

（2）∵一次函数y=x-3与x轴相交于点B，

∴x-3=0，

解得x=2，

∴点B的坐标为（2，0），

如图，过点A作AE⊥x轴，垂足为E，过点D作DF⊥x轴，垂足为F，

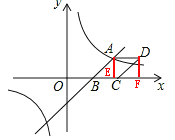
∵A（4，3），B（2，0），

∴OE=4，AE=3，OB=2，

∴BE=OE-OB=4-2=2，

在Rt△ABE中，

AB=，

∵四边形ABCD是菱形，

∴AB=CD=BC=，AB∥CD，

∴∠ABE=∠DCF，

∵AE⊥x轴，DF⊥x轴，

∴∠AEB=∠DFC=90°，

在△ABE与△DCF中，

，

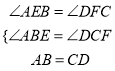∴△ABE≌△DCF（ASA），

∴CF=BE=2，DF=AE=3，

∴OF=OB+BC+CF=2++2=4+，

∴点D的坐标为（4+，3）．

（3）当y=-2时，-2=，解得x=-6．

故当y≥-2时，自变量x的取值范围是x≤-6或x＞0．