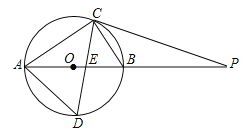
【题目】如图,AB为⊙O的直径,C为⊙O上一点,D、E分别是∠ACB的平分线与⊙O、AB的交点,P为AB延长线上一点,且PC=PE.试判断直线PC与⊙O的位置关系,并说明理由.
参考答案:
【答案】直线PC与⊙O相切.证明见解析.
【解析】试题分析:连结OC,由PC=PE得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠A+∠ACE=∠A+45°,加上∠A=90°-∠ABC,∠ABC=∠OCB,于是可得到∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,则∠OCE+∠PCE=90°,于是根据切线的判定定理可得PC为⊙O的切线
试题解析:直线PC与⊙O相切.
理由:连接OC
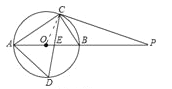
∵PC=PE
∴∠PCE=∠PEC
∴∠PCB+∠BCE=∠ACE+∠CAE
∵CD平分∠ACB
∴∠BCE=∠ACE
∴∠PCB=∠CAE
∵AB为直径
∴∠ACB=90°
∴∠CAE+∠CBA=90°
∴∠PCB+∠CBA=90°
∵OC=OB
∴∠OCB=∠CBA
∴∠PCB+∠OCB =90°,即∠OCP=90°
∴直线PC与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D.下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有
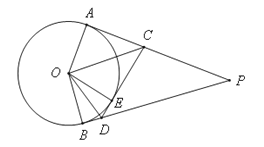
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(2-a)x2+x+a2-4=0的一个根为0,则a的值为( )
A.2B.0C.2或-2D.-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面一列分式:
 , ﹣
, ﹣ ,
,  , ﹣
, ﹣ , …(其中x≠0).
, …(其中x≠0).
(1)根据上述分式的规律写出第6个分式;
(2)根据你发现的规律,试写出第n(n为正整数)个分式,并简单说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )
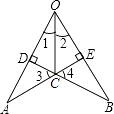
A.2对
B.3对
C.4对
D.5对 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+3x=-1的常数项是 _________.
相关试题

