【题目】某市为了建设国家级卫生城市.市政部门决定搭配A、B两种园艺造型共50个摆放在市区,现有3490盆甲种花卉和2950盆乙种花卉可供使用,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个A种造型的费用是800元,搭配一个B种造型的费用是960元,试说明(1)中哪种方案费用最低?最低费用是多少元?
参考答案:
【答案】(1)方案一:31个A、19个B,方案二:32个A、18个B,方案三:33个A、17个B;(2)42720元
【解析】
(1)摆放50个园艺造型所需的甲种和乙种花卉应<现有的盆数,可由此列出不等式求出符合题意的搭配方案来;
(2)根据两种造型单价的成本费可分别计算出各种可行方案所需的成本,然后进行比较;也可由两种造型的单价知单价成本较低的造型较多而单价成本较高的造型较少,所需的总成本就低.
解:(1)设搭配A种造型x个,则B种造型为(50﹣x)个,根据题意
![]() ,
,
解之得:![]()
∵x是整数,
∴x可取31,32,33
∴可设计三种搭配方案,分别为:
方案一:31个A,19个B;
方案二:32个A,18个B;
方案三:33个A,17个B.
(2)如果一个A造型费用800元,一个B造型费用960元,则各个方案费用分别为:
方案一,31×800+19×960=43040元
方案二,32×800+18×960=42880元
方案三,33×800+17×960=42720元
通过上述计算发现,方案三费用最低,最低为42720元
-
科目: 来源: 题型:
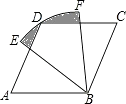
查看答案和解析>>【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
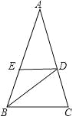
A. 1个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
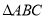 中,
中,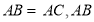 的垂直平分线交
的垂直平分线交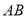 于
于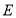 ,交
,交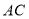 所在直线于
所在直线于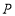 ,若
,若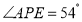 ,则
,则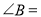 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.

(1)当DE∥BC时,△ACD的形状按角分类是直角三角形;
(2)在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 的三个顶点的坐标分别为
的三个顶点的坐标分别为
(1)请按下列要求画图:
①将
 先向右平移
先向右平移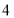 个单位长度、再向上平移
个单位长度、再向上平移 个单位长度,得到
个单位长度,得到 ,画出
,画出
②
 与
与 关于原点
关于原点 成中心对称,画出
成中心对称,画出
③画出
 绕点
绕点 顺时针旋转
顺时针旋转 后得到的
后得到的
(2)在
 中所得的
中所得的 和
和 关于点
关于点 成中心对称,请直接写出对称中心
成中心对称,请直接写出对称中心 点的坐标.
点的坐标.
相关试题

