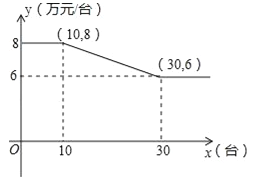
【题目】某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
(1)当x=10时,公司销售机器人的总利润为 万元;
(2)当10≤x≤30时,求出y与x的函数关系式;
(3)问:销售量为多少台时,公司销售机器人的总利润为37.5万元.
参考答案:
【答案】(1)20;(2)![]() ;(3)15.
;(3)15.
【解析】
试题分析:(1)由“总利润=单台利润×销售数量”结合图象即可得出结论;
(2)设y与x之间的函数关系式为y=kx+b,由函数图象找出点的坐标,再利用待定系数法即可求出结论;
(3)设销售量为m台时,公司销售机器人的总利润为37.5万元.分析销售利润为37.5万元时,销售台数m的范围,再结合此时进价y与x的函数关系式得出销售m台时的进价,再由“总利润=单台利润×销售数量”即可得出关于m的一元二次方程,解方程即可得出结论..
试题解析:(1)当x=10时,公司销售机器人的总利润为10×(10﹣8)=20(万元).
故答案为:20.
(2)设y与x之间的函数关系式为y=kx+b,∵函数图象过点(10,8),(30,6),∴有![]() ,解得:
,解得: ,∴当10≤x≤30时,y与x的函数关系式为
,∴当10≤x≤30时,y与x的函数关系式为![]() .
.
(3)设销售量为m台时,公司销售机器人的总利润为37.5万元.
∵37.5>20,∴m>10,又∵m为正整数,∴4m≠37.5,∴只有在10<m<30内,公式销售机器人的总利润才有可能为37.5万元.
依题意得:m[10﹣(![]() )]=37.5,解得:m1=15,m2=﹣25(舍去).
)]=37.5,解得:m1=15,m2=﹣25(舍去).
答:销售量为15台时,公司销售机器人的总利润为37.5万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出数轴,把22 , 0,﹣2,(﹣1)3 , ﹣|﹣3.5|,
 这六个数在数轴上表示出来;按从小到大的顺序用“<”号将各数连接起来.
这六个数在数轴上表示出来;按从小到大的顺序用“<”号将各数连接起来. -
科目: 来源: 题型:
查看答案和解析>>【题目】十边形的内角和是度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型
价格A型
B型
进价(元/盏)
40
65
标价(元/盏)
60
100
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为( )
A. 4 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
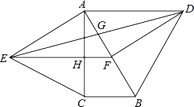
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为(请将所有正确的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
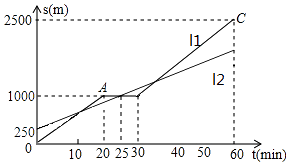
(1)图中线(填l1或l2)表示的是爸爸所走路程与步行时间的函数关系式.
(2)请分别求出l1中BC段以及l2的函数关系式.
(3)请求出小明出发多少时间与爸爸第最后一次相遇.
(4)在速度不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整.
相关试题

