【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?
参考答案:
【答案】
(1)解:设A型台灯购进x盏,B型台灯购进y盏.
根据题意得: ![]() ,解得:
,解得: ![]()
(2)解:30×(60×90%﹣40)+20×(100×80%﹣65)
=30×14+20×15
=720(元).
答:A型台灯购进30盏,B型台灯购进20盏;这批台灯全部售完后,商场共获利720元.
【解析】(1)有两个等量关系:A型灯盏数+B型灯盏数=50,购买A型灯钱数+购买B型灯钱数=2500.(2)根据利润=售价﹣进价,知商场共获利=A型灯利润+B型灯利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个底面半径为10cm,高为30cm的圆柱形大杯中存满了水,把水倒入一个底面直径为10cm的圆柱形小杯中,刚好倒满12杯,则小杯的高为()
A. 12cm B. 10cm C. 6cm D. 5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出数轴,把22 , 0,﹣2,(﹣1)3 , ﹣|﹣3.5|,
 这六个数在数轴上表示出来;按从小到大的顺序用“<”号将各数连接起来.
这六个数在数轴上表示出来;按从小到大的顺序用“<”号将各数连接起来. -
科目: 来源: 题型:
查看答案和解析>>【题目】十边形的内角和是度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
(1)当x=10时,公司销售机器人的总利润为 万元;
(2)当10≤x≤30时,求出y与x的函数关系式;
(3)问:销售量为多少台时,公司销售机器人的总利润为37.5万元.
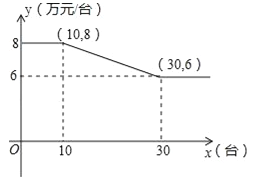
-
科目: 来源: 题型:
查看答案和解析>>【题目】一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为( )
A. 4 B. 6 C. 8 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为(请将所有正确的序号都填上).
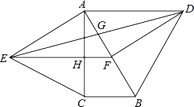
相关试题

