【题目】(1)用配方法解方程:x2﹣2x﹣1=0.
(2)解方程:2x2+3x﹣1=0.
(3)解方程:x2﹣4=3(x+2).
参考答案:
【答案】(1)x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ;(2)x1=
;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=﹣2,x2=5.
;(3)x1=﹣2,x2=5.
【解析】试题分析:(1)按要求利用配方法进行求解即可;
(2)利用公式法进行求解即可;
(3)整体移项后利用因式分解法进行求解即可.
试题解析:(1)x2-2x-1=0,
x2-2x=1,
x2-2x+1=1+1,
(x-1)2=2,
x-1=![]() ,
,
x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ;
;
(2)2x2+3x﹣1=0,
a=2,b=3,c=-1,
b2-4ac=9+8=17>0,
x=![]() ,
,
x1=![]() ,x2=
,x2=![]() ;
;
(3)x2﹣4=3(x+2),
(x+2)(x-2)-3(x+2)=0,
(x+2)(x-2-3)=0,
x1=﹣2,x2=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=
 +1,求BC的长.
+1,求BC的长.
-
科目: 来源: 题型:
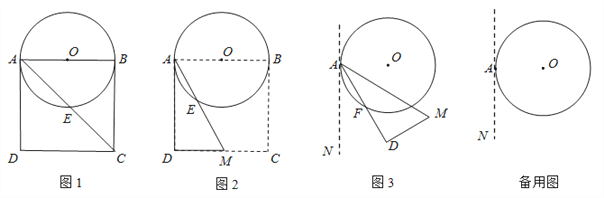
查看答案和解析>>【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
(1)线段AE=____________;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α=___________°时,DM与⊙O相切。
-
科目: 来源: 题型:
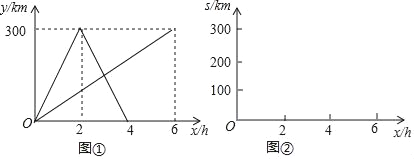
查看答案和解析>>【题目】快车和慢车同时从甲地出发,匀速行驶,快车到达乙地后,原路返回甲地,慢车到达乙地停止.图①表示两车行驶过程中离甲地的路程y(km)与出发时间x(h)的函数图象,请结合图①中的信息,解答下列问题:
(1)快车的速度为 km/h,慢车的速度为 km/h,甲乙两地的距离为 km;
(2)求出发多长时间,两车相距100km;
(3)若两车之间的距离为s km,在图②的直角坐标系中画出s(km)与x(h)的函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
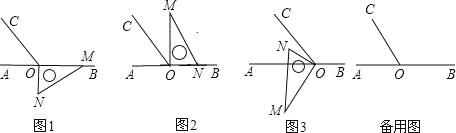
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在由边长为1的小正方形组成的网格图中有△ABC,建立平面直角坐标系后,点O的坐标是(0,0).
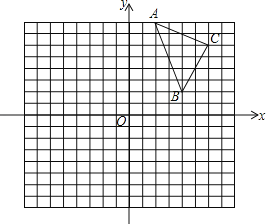
(1)以O为位似中心,作△A′B′C′∽△ABC,相似比为1:2,且保证△A′B′C′在第三象限;
(2)点B′的坐标为( , );
(3)若线段BC上有一点D,它的坐标为(a,b),那么它的对应点D′的坐标为( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
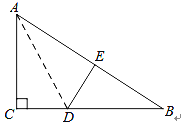
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
相关试题

