【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
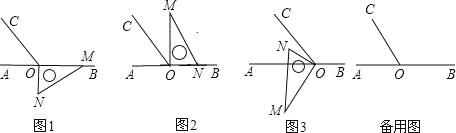
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
参考答案:
【答案】(1)90 (2)答案见解析 (3)4秒或16秒
【解析】
(1)根据旋转的性质知,旋转角是∠MON;
(2)如图3,利用平角的定义,结合已知条件“∠AOC:∠BOC=1:2”求得∠AOC=60°;然后由直角的性质、图中角与角间的数量关系推知∠AOM﹣∠NOC=30°;
(3)需要分类讨论:(ⅰ)当直角边ON在∠AOC外部时,旋转角是60°;(ⅱ)当直角边ON在∠AOC内部时,旋转角是240°
解:(1)由旋转的性质知,旋转角∠MON=90°.
故答案是:90;
(2)如图3,∠AOM﹣∠NOC=30°.
设∠AOC=α,由∠AOC:∠BOC=1:2可得
∠BOC=2α.
∵∠AOC+∠BOC=180°,
∴α+2α=180°.
解得 α=60°.
即∠AOC=60°.
∴∠AON+∠NOC=60°.①
∵∠MON=90°,
∴∠AOM+∠AON=90°.②
由②﹣①,得∠AOM﹣∠NOC=30°;
(3)(ⅰ)如图4,当直角边ON在∠AOC外部时,
由OD平分∠AOC,可得∠BON=30°.
因此三角板绕点O逆时针旋转60°.
此时三角板的运动时间为:
t=60°÷15°=4(秒).
(ⅱ)如图5,当直角边ON在∠AOC内部时,
由ON平分∠AOC,可得∠CON=30°.
因此三角板绕点O逆时针旋转240°.
此时三角板的运动时间为:
t=240°÷15°=16(秒).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC的两条角平分线相交于一点G,∠BAC=76°,∠ABE=20°,求∠BEC,∠ADC的度数.
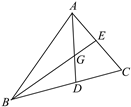
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是△ABC内一点,连结BP,并延长交AC于点D.
(1)试探究AB+BC+CA与2BD的大小关系;
(2)试探究AB+CA与PB+PC的大小关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲、乙两种型号的机器生产同样的产品,两种型号的机器一共48台,其中甲型号机器比乙型号机器多10台.
(1)乙型号机器有 台(请直接写出答案);
(2)若已知4台甲型号机器一天生产的产品装满6箱后还剩8个,5台乙型号机器的产品还缺1个就可以装满8箱,每台甲型号机器比每台乙型号机器一天多生产1个产品,求每箱装多少个产品?
(3)在前两问的条件下,若某天有2台甲型号机器和若干台乙型号机器同时开工,问这天生产的产品能否恰好装满35箱,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂分别安排甲乙两个车间加工1000个同一型号的奥运会吉祥物,每名工人每天加工吉祥物的个数相等且保持不变,由于生产需要,其中一个车间推迟两天开始加工,刚开始加工时,甲车间有10名工人,乙车间有12名工人,图中线段OB和折线ACB分别表示两个车间的加工情况.依据图中提供的信息,完成下列各题:
(1)线段OB反映的是 车间的加工情况;
(2)开始加工后,甲车间加工多少天后,两车间加工吉祥物数相同?
(3)根据折线段反映的加工情况,请你提出一个问题,并给出解答.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l1,l2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是
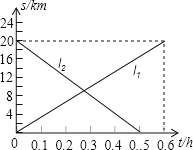
A. 乙摩托车的速度较快
B. 经过0.3小时甲摩托车行驶到A,B两地的中点
C. 经过0.25小时两摩托车相遇
D. 当乙摩托车到达A地时,甲摩托车距离A地
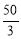 km
km
相关试题

