【题目】如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4)
(1)求直线BD和抛物线对应的函数解析式;
(2)在抛物线对称轴上求一点P的坐标,使△ABP的周长最小;
(3)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为点N,使得以M,O,N为顶点的三角形与△BOC相似?若存在,求出点M的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=-2x+2,y=-x2+x+2;(2)(![]() );(3)存在,M(1,2)或
);(3)存在,M(1,2)或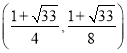 .
.
【解析】试题分析:(1)利用直线与坐标轴的交点坐标,求出抛物线的解析式,利用翻折得出点C的坐标,就可求出直线BD的解析式;(2)本题利用路径最短的知识来解决问题;(3)由(1)的解析式设M(a,-a2+a+2),当△BOC∽△MON或△BOC∽△ONM时,由相似三角形的性质就可以求出结论.
试题解析:(1)易得A(-1,0),B(0,2),C(1,0).
设直线BD对应的函数解析式为y=kx+m.
把B(0,2),C(1,0)的坐标分别代入y=kx+m,
得![]() 解得
解得![]()
∴直线BD对应的函数解析式为y=-2x+2.
∵抛物线对应的函数解析式为y=-x2+bx+c.
∴把B(0,2),D(3,-4)的坐标分别代入y=-x2+bx+c,
得![]() 解得
解得![]()
∴抛物线对应的函数解析式为y=-x2+x+2.
(2)对称轴为:点A(-1,0)关于对称轴的对称点为E(2.0),连接BE交对称轴与点P,则BE的解析式为:y=-x+2 ,当x=![]() 时,BE与对称轴的交点坐标是P:(
时,BE与对称轴的交点坐标是P:(![]() ).
).
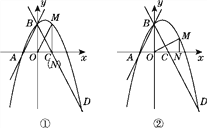
(3)存在,①如图①,当△MON∽△BCO时,![]() =
=![]() ,即
,即![]() =
=![]() ,∴MN=2ON.设ON=a,则M(a,2a),∴-a2+a+2=2a,解得a1=-2(不合题意,舍去),a2=1,∴M(1,2);②如图②,当△MON∽△CBO时,
,∴MN=2ON.设ON=a,则M(a,2a),∴-a2+a+2=2a,解得a1=-2(不合题意,舍去),a2=1,∴M(1,2);②如图②,当△MON∽△CBO时,![]() =
=![]() ,即
,即![]() =
=![]() ,∴MN=
,∴MN=![]() ON.设ON=n,则M
ON.设ON=n,则M![]() ,∴-n2+n+2=
,∴-n2+n+2=![]() ,解得n1=
,解得n1=![]() (不合题意,舍去),n2=
(不合题意,舍去),n2=![]() ,∴M(
,∴M(![]() ,
,![]() ).∴存在这样的点M(1,2)或
).∴存在这样的点M(1,2)或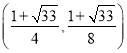 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系内的点P(x2﹣3x,4)与另一点Q(x﹣8,y)关于原点对称,则x+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若用A(2,1)表示放置2个胡萝卜,1棵小白菜;点B(4,2)表示放置4个胡萝卜,2棵小白菜:

(1)请你写出C、E所表示的意义.
(2)若一只兔子从A顺着方格线向上或向右移动到达B,试问有几条路径可供选择,其中走哪条路径吃到的胡萝卜最多?走哪条路径吃到的小白菜最多?请你通过计算的方式说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的余角是30°,那么这个角是 .
-
科目: 来源: 题型:
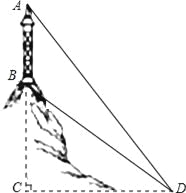
查看答案和解析>>【题目】如图,山顶有一铁塔AB的高度为20米,为测量山的高度BC,在山脚点D处测得塔顶A和塔基B的仰角分别为60°和45°.求山的高度BC.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+5x+2=0的两个实数根为x1,x2,则x1+x2=_____.
相关试题

