【题目】如图,在平面直角坐标系中, ![]() ,
, ![]() 两点的坐标分别为
两点的坐标分别为![]() ,
, ![]() ,连接
,连接![]() ,若以点
,若以点![]() ,
, ![]() ,
, ![]() 为顶点的三角形是等腰直角三角形,则点
为顶点的三角形是等腰直角三角形,则点![]() 坐标为__________.
坐标为__________.

参考答案:
【答案】![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
【解析】∵A、B两点的坐标分别为(-4,0)、(0,2)
∴OA=4,OB=2.
(1)如图,当∠APB=90°时,作PE⊥OA于点E,
易证△APE≌△BPD,则PD=PE=OE=OD,AE=BD,
设PD= ![]() ,
,
则![]() ,解得:
,解得: ![]() ,
,
∴此时点P的坐标为(-3,3);
同理可得:点P1的坐标为(-1,-1).
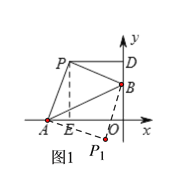
(2)如图2,当∠ABP=90°时,作PD⊥OB于点D,
易证△ABO≌△BPD,则PD=OB=2,BD=AO=4,
∴OD=OB+BD=6,
∴点P的坐标为(-2,6).
同理可得P2的坐标为(2,-2).
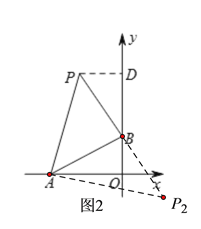
(3)如图3,过点P作PD⊥OA于点D,
易证△PDA≌△AOB,则AD=BO=2,PD=AO=4,
∴OD=AD+OA=6,
∴点P的坐标为(-6,4).
同理可得点P3的坐标为(-2,-4).
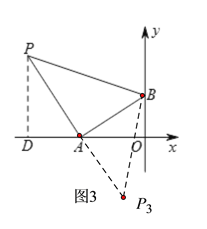
综上所述,若△PAB为等腰直角三角形,则点P的坐标为:(-3,3)、(-1,-1)、(-2,6)、(2,-2)、(-6,4)和(-2,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程或方程组:
(1) 3 = 1-2(4+x);(2)
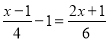
(3)
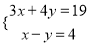 ;(4)
;(4)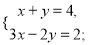
-
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+
 a2b+3,B=﹣
a2b+3,B=﹣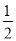 a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣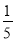 (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.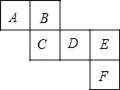
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,∠AOB=∠COD=90°,射线OE,FO分别平分∠AOC和∠BOD.
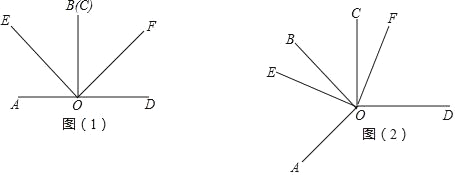
(1)当OB和OC重合时,如图(1),求∠EOF的度数;
(2)当∠AOB绕点O逆时针旋转至图(2)的位置(0°<∠BOC<90°)时,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
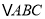 与
与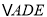 都是以
都是以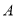 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形, 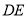 交
交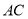 于点
于点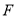 ,若
,若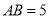 ,
, 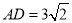 ,当
,当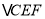 是直角三角形时,则
是直角三角形时,则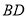 的长为__________.
的长为__________.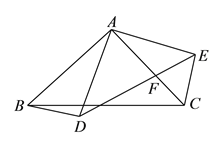
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
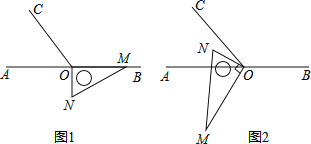
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
相关试题

