【题目】解下列方程或方程组:
(1) 3 = 1-2(4+x);(2) ![]()
(3) ![]() ;(4)
;(4)![]()
参考答案:
【答案】①x=-5;(2)-17 ;(3)![]() ;(4)
;(4)![]()
【解析】试题分析:(1) 去括号、移项、合并同类项的法则求出x的值即可;
(2)根据去分母、去括号、移项、合并同类项的法则求出x的值即可;
(3)运用加减消元法解;
(3)运用加减消元法解.
试题解析:
(1) 3 = 1-2(4+x)
-8-2x+1=3
-2x=10
x=-5.
(2) ![]()
3(x-1)-12=2(2x+1)
3x-3-12=4x+2
-x=17
x=-17.
(3) ![]()
由②![]() 4得:4x-4y=16③
4得:4x-4y=16③
由③+①得:7x=35
x=5
把x=5代入②得,y=1
所以方程组的解为![]() .
.
(4) ![]()
由①![]() 2得:2x+2y=8③
2得:2x+2y=8③
由②+③是:5x=10
x=2
把x=2代入①得y=2,
所以方程组的解为![]() .
.
-
科目: 来源: 题型:
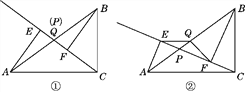
查看答案和解析>>【题目】已知点P是Rt△ABC斜边AB上一动点(不与点A,B重合),分别过点A,B向直线CP作垂线,垂足分别为点E,F,点Q为斜边AB的中点.
(1)如图①,当点P与点Q重合时,AE与BF的位置关系是________,QE与QF的数量关系是________;
(2)如图②,当点P在线段AB上且不与点Q重合时,试判断QE与QF的数量关系,并说明理由.
(温馨提示:直角三角形斜边上的中线等于斜边的一半)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
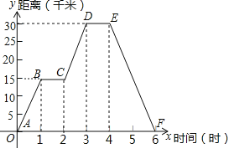
(1)根据图象回答:小明到达离家最远的地方需 小时,
(2)小明出发两个半小时离家 千米.
(3)小明出发 小时离家12千米.
-
科目: 来源: 题型:
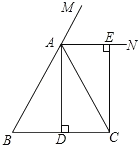
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一个正方体的表面展开图,请回答下列问题:
(1)与面B,C相对的面分别是 ;
(2)若A=a3+
 a2b+3,B=﹣
a2b+3,B=﹣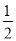 a2b+a3,C=a3﹣1,D=﹣
a2b+a3,C=a3﹣1,D=﹣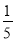 (a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.
(a2b+15),且相对两个面所表示的代数式的和都相等,求E,F分别代表的代数式.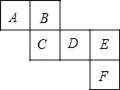
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,
,  两点的坐标分别为
两点的坐标分别为 ,
,  ,连接
,连接 ,若以点
,若以点 ,
,  ,
,  为顶点的三角形是等腰直角三角形,则点
为顶点的三角形是等腰直角三角形,则点 坐标为__________.
坐标为__________.
相关试题

