【题目】(提出问题)课间,一位同学拿着方格本遇人便问:“如图所示,在边长为1的小正方形组成的网格中,点A、B、C都是格点,如何证明点A、B、C在同一直线上呢?”

(分析问题)一时间,大家议论开了. 同学甲说:“可以利用代数方法,建立平面直角坐标系,利用函数的知识解决”,同学乙说:“也可以利用几何方法…”同学丙说:“我还有其他的几何证法”……
(解决问题)请你用两种方法解决问题
方法一(用代数方法):

方法二(用几何方法):

参考答案:
【答案】(1)见详解;(2)见详解.
【解析】
(1)以点B为原点建立平面直角坐标系,则点C为(1,2),利用待定系数法求出直线BC的解析式,然后判断点A是否在直线BC上即可;
(2)在格点中构造两个三角形,证明△ABD≌△BCE,得到∠ABD=∠BCE,利用平角的定义,得到∠ABC=180°,即可得到点A、B、C在同一条直线上.
解:(1)如图,以点B为原点建立平面直角坐标系,
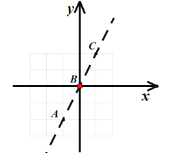
则点C坐标为(1,2),
设直线BC的解析式为:![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为:![]() ;
;
当![]() 时,
时,![]() ,
,
∴点A(![]() )在直线BC上,
)在直线BC上,
∴A、B、C三点在同一条直线上;
(2)如图,在网格中构造两个三角形,△ABD和△BCE;
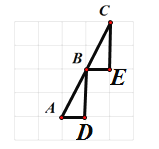
∵网格的边长为1,
∴AD=BE=1,BD=CE=2,∠D=∠E=90°,
∴△ABD≌△BCE,
∴∠ABD=∠BCE,
∵∠BCE+∠CBE=90°,
∴∠ABD+∠CBE=90°,
∴∠ABC=∠ABD+∠DBE+∠CBE=90°+90°=180°,
∴A、B、C三点在同一条直线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,点A、B分别在边ON和OM上(∠OAB≠45°).

(1)根据要求,利用尺规作图,补全图形:
第①步:作∠MON的平分线OC,作线段AB的垂直平分线l,OC和l交于点P,第②步:连接PA、PB;
(2)结合补完整的图形,判断PA和PB有什么数量关系和位置关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进A,B两种新型节能台灯共80盏,这两种台灯的进价、售价如下表所示:

(1)若商场的进货款为3700元,则这两种台灯各购进了多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的2倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )

A. ac>0 B. 当x>0时,y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1,x2=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c的顶点M在第二象限,且经过点 A(1,0)和点 B(0,2).则
(1)a 的取值范围是________;
(2)若△AMO的面积为△ABO面积的
 倍时,则a的值为________
倍时,则a的值为________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是_____.
(1)EF=
 OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE= ;(4)OGBD=AE2+CF2.
;(4)OGBD=AE2+CF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
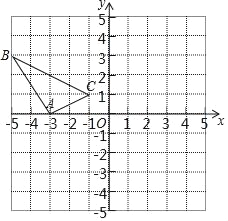
相关试题

