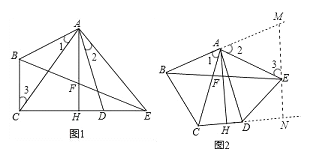
【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.

参考答案:
【答案】(1)详见解析;(2)结论仍然成立,理由详见解析.
【解析】
试题分析:(1)①根据已知条件,利用SAS即可判定△ABC≌△ADE;②易证BC∥FH和CH=HE,根据平行线分线段成比例定理可证得BF=EF.(2)过E作MN⊥AH,交BA、CD延长线于M、N,,利用ASA证明△MAE≌△DAC,得AD=AM,根据等量代换得AB=AM,根据②同理得出结论.
试题解析:证明:(1)①如图1,
∵AB⊥AD,AE⊥AC,
∴∠BAD=90°,∠CAE=90°,
∴∠1=∠2,
在△ABC和△ADE中,
∵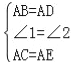
∴△ABC≌△ADE(SAS);
②如图1,
∵△ABC≌△ADE,
∴∠AEC=∠3,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AH⊥CD,AE=AC,
∴CH=HE,
∵∠AHE=∠BCE=90°,
∴BC∥FH,
∴![]() =1,
=1,
∴BF=EF;
(2)结论仍然成立,理由是:
如图2所示,过E作MN⊥AH,交BA、CD延长线于M、N,
∵∠CAE=90°,∠BAD=90°,
∴∠1+∠2=90°,∠1+∠CAD=90°,
∴∠2=∠CAD,
∵MN∥AH,
∴∠3=∠HAE,
∵∠ACH+∠CAH=90°,∠CAH+∠HAE=90°,
∴∠ACH=∠HAE,
∴∠3=∠ACH,
在△MAE和△DAC中,
∵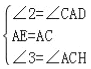
∴△MAE≌△DAC(ASA),
∴AM=AD,
∵AB=AD,
∴AB=AM,
∵AF∥ME,
∴![]() =1,
=1,
∴BF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的方程kx2﹣6x+9=0有两个相等的实数根,那么k的值为_____.
-
科目: 来源: 题型:
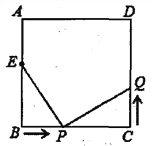
查看答案和解析>>【题目】如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以4cm/秒的速度由B点向C点运动,同时,点Q在线段CD上以acm/秒的速度由C点向D点运动,设运动的时间为t秒,
(1)CP的长为 cm(用含t的代数式表示);
(2)若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,求a的值.
(3)若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动.则点P与点Q会不会相遇?若不相遇,请说明理由.若相遇,求出经过多长时间点P与点Q第一次在正方形ABCD的何处相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1_____y2.(填“>”“<”或“=”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内,把一个图形整体沿着某一移动,会得到一个新的图形,这种移动叫做 , 是运动的一种形式,是图形变换的一种。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=﹣2x+b经过点(3,5),则关于x的不等式﹣2x+b<5的解集是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平移是由平移的和平移的决定的,所以在平移作图时,首先要明确图形原来的位置及平移的,再进行画图.
相关试题

