【题目】在平面直角坐标系xOy中,直线![]() 与y轴交于点A.
与y轴交于点A.
(1)如图,直线![]() 与直线
与直线![]() 交于点B,与y轴交于点C,点B横坐标为
交于点B,与y轴交于点C,点B横坐标为![]() .
.
①求点B的坐标及k的值;
②直线![]() 与直线
与直线![]() 与y轴所围成的△ABC的面积等于 ;
与y轴所围成的△ABC的面积等于 ;
(2)直线![]() 与x轴交于点E(
与x轴交于点E(![]() ,0),若
,0),若![]() ,求k的取值范围.
,求k的取值范围.

参考答案:
【答案】(1)①(-1,3),1;②![]() ;(2)2<k<4.
;(2)2<k<4.
【解析】
试题(1)①将x=-1代入y=-2x+1,得出B点坐标,进而求出k的值;
②求出A,C点坐标,进而得出AC的长,即可得出△ABC的面积:
∵k=1,∴一次函数解析式为:y="x+4." ∴A(0,4).
∵y=-2x+1,∴C(0,1).∴AC=4-1=3.
∴△ABC的面积为:![]() ×1×3=
×1×3=![]() .
.
(2)分别得出当x0=-2以及-1时k的值,进而得出k的取值范围.
试题解析:解:(1)①∵直线y=-2x+1过点B,点B的横坐标为-1,∴y=2+2=3.
∴B(-1,3).
∵直线y=kx+4过B点,
∴3=-k+4,解得:k=1.
②![]() .
.
(2)∵直线y=kx+4(k≠0)与x轴交于点E(x0,0),![]() ,
,
∴当x0=-2,则E(-2,0),代入y=kx+4得:0=-2k+4,解得:k=2.
当x0=-1,则E(-1,0),代入y=kx+4得:0=-k+4,解得:k=4.
∴k的取值范围是:2<k<4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

-
科目: 来源: 题型:
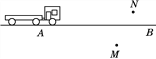
查看答案和解析>>【题目】如图,M,N为坐落于公路两旁的村庄,如果一辆施工的机动车由A向B行驶,产生的噪音会对两个村庄造成影响.
(1)当施工车行驶到何处时,产生的噪音分别对两个村庄影响最大?在图中标出来.
(2)当施工车从A向B行驶时,产生的噪音对M,N两个村庄的影响情况如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师的数学课采用小组合作学习的方式,把班上40名学生分成若干个小组.如果要求每小组只能是5人或6人,那么分组方案有( )
A. 4种 B. 3种 C. 2种 D. 1种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车
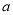 辆,B型车
辆,B型车 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用 ﹣1来表示
﹣1来表示 的小数部分,事实上,小明的表示方法是有道理的,因为
的小数部分,事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是
的整数部分是1,将这个数减去其整数部分,差就是 的小数部分,又例如:∵22<(
的小数部分,又例如:∵22<( )2<32,即2<
)2<32,即2< <3,∴
<3,∴ 的整数部分为2,小数部分为(
的整数部分为2,小数部分为( ﹣2).
﹣2).请解答:
(1)
 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .(2)如果
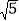 的小数部分为a,
的小数部分为a, 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣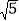 的值.
的值.(3)已知x是3+
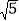 的整数部分,y是其小数部分,直接写出x﹣y的值.
的整数部分,y是其小数部分,直接写出x﹣y的值.
相关试题

