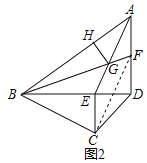
【题目】如图1,四边形ABCD中,BD⊥AD,E为BD上一点,AE=BC,CE⊥BD,CE=ED

(1)已知AB=10,AD=6,求CD;
(2)如图2,F为AD上一点,AF=DE,连接BF,交BF交AE于G,过G作GH⊥AB于H,∠BGH=75°.求证:BF=2![]() GH+
GH+![]() EG.
EG.
参考答案:
【答案】(1)2![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)由勾股定理得出BD=![]() =8,由HL证得Rt△ADE≌Rt△BEC,得出BE=AD,则CE=ED=BD﹣BE=BD﹣AD=2,由等腰直角三角形的性质即可得出结果;
=8,由HL证得Rt△ADE≌Rt△BEC,得出BE=AD,则CE=ED=BD﹣BE=BD﹣AD=2,由等腰直角三角形的性质即可得出结果;
(2)连接CF,易证AF=CE,AD∥CE,得出四边形AECF是平行四边形,则AE=CF,AE∥CF,得出∠CFD=∠EAD,∠CFB=∠AGF,由Rt△ADE≌Rt△BEC,得出∠CBE=∠EAD,推出∠CBE=∠CFD,证得△BCF是等腰直角三角形,则BF=![]() BC=
BC=![]() CF=
CF=![]() AE,∠FBC=∠BFC=45°,推出∠AGF=45°,∠AGH=60°,∠GAH=30°,则AG=2GH,得出BF=
AE,∠FBC=∠BFC=45°,推出∠AGF=45°,∠AGH=60°,∠GAH=30°,则AG=2GH,得出BF=![]() AE=
AE=![]() (AG+EG),即可得出结论.
(AG+EG),即可得出结论.
(1)解:∵BD⊥AD,
∴BD=![]() =
=![]() =8,
=8,
∵CE⊥BD,
∴∠CEB=∠EDA=90°,
在Rt△ADE和Rt△BEC中,![]() ,
,
∴Rt△ADE≌Rt△BEC(HL),
∴BE=AD,
∴CE=ED=BD﹣BE=BD﹣AD=8﹣6=2,
∴CD![]() =CE=2
=CE=2![]() ;
;
(2)解:连接CF,如图2所示:
∵AF=DE,DE=CE,
∴AF=CE,
∵BD⊥AD,CE⊥BD,
∴AD∥CE,
∴四边形AECF是平行四边形,
∴AE=CF,AE∥CF,
∴∠CFD=∠EAD,∠CFB=∠AGF,
由(1)得:Rt△ADE≌Rt△BEC,
∴∠CBE=∠EAD,
∴∠CBE=∠CFD,
∵∠FBD+∠BFC+∠CFD=90°,
∴∠FBD+∠BFC+∠CBE=90°,
∴∠BCF=90°,
∵AE=BC,
∴BC=CF,
∴△BCF是等腰直角三角形,
∴BF=![]() BC=
BC=![]() CF=
CF=![]() AE,∠FBC=∠BFC=45°,
AE,∠FBC=∠BFC=45°,
∴∠AGF=45°,
∵∠BGH=75°,
∴∠AGH=180°﹣45°﹣75°=60°,
∵GH⊥AB,
∴∠GAH=30°,
∴AG=2GH,
∴BF=![]() AE=
AE=![]() (AG+EG),
(AG+EG),
∴BF=2![]() GH+
GH+![]() EG.
EG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),
 的顶点
的顶点 、
、 、
、 分别与正方形
分别与正方形 的顶点
的顶点 、
、 、
、 重合.
重合.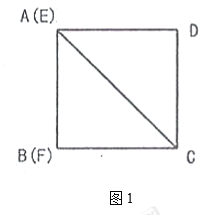
(1)若正方形的边长为
 ,用含
,用含 的代数式表示:正方形
的代数式表示:正方形 的周长等于_______,
的周长等于_______, 的面积等于_______.
的面积等于_______.(2)如图2,将
 绕点
绕点 顺时针旋转,边
顺时针旋转,边 和正方形的边
和正方形的边 交于点
交于点 .连结
.连结 ,设旋转角
,设旋转角 .
.
①试说明
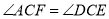 ;
; ②若
 有一个内角等于
有一个内角等于 ,求
,求 的值.
的值. -
科目: 来源: 题型:
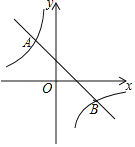
查看答案和解析>>【题目】如图,一次函数y1=kx+2图象与反比例函数y2=
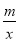 图象相交于A,B两点,已知点B的坐标为(3,﹣1).
图象相交于A,B两点,已知点B的坐标为(3,﹣1).(1)求一次函数和反比例函数的解析式;
(2)请直接写出不等式kx﹣
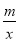 ≤﹣2的解集;
≤﹣2的解集;(3)点C为x轴上一动点,当S△ABC=3时,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】西南大学银翔实验中学第二届缤纷科技节于2019年5月份隆重举行,主题:绿色体验成长﹣玩出你的稀缺竞争力,本届缤纷科技节有展示类、体验类、竞赛类共40多个项目.4月份,学校对活动中所需物品统一购,其中某一体验类项目需要A、B两种材料,已知A种材料单价32元/套,B种材料单价24元/套,活动需要A、B两种材料共50套计划购买A、B两种材料总费用不超过1392元.
(1)若按计划采购,最多能购买A种材料多少套?
(2)在实际来购过程中,受多方面因素的影响,与(1)中最多购买A种材料的计划相比,实际采购A种材料数量的增加了
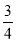 a%,B种材料的数量减少
a%,B种材料的数量减少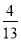 a%(A、B材料的数量均为整数),实际采购A种材料的单价减少了
a%(A、B材料的数量均为整数),实际采购A种材料的单价减少了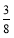 a%,B种材料的单价增加
a%,B种材料的单价增加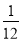 a%,且实际总费用比按(1)中最多购买A种材料的总费用多了16元,求a.
a%,且实际总费用比按(1)中最多购买A种材料的总费用多了16元,求a. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE丄AB,垂足为D,EF//AC,

(1)求
 的度数;
的度数;(2)连接BE,若BE同时平分
 和
和 ,问EF与BF垂直吗? 为什么?
,问EF与BF垂直吗? 为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
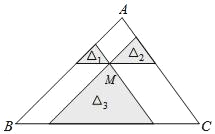
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

相关试题

