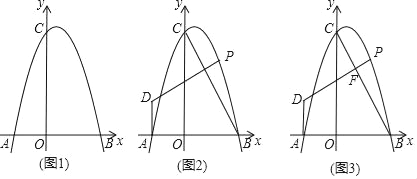
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.
参考答案:
【答案】(1)a=-1,b=1;(2)d=﹣t2+![]() t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣
t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).
【解析】试题分析:
(1)把A、B两点的坐标代入抛物线的解析式列出关于a、b的二元一次方程组,解方程组即可求得a、b的值;
(2)如下图2、过点P作PG⊥DE于点K,交x轴于点G,作DK⊥PG于点K,则由已知条件易得∠BCO=∠PDK,由此可得tan∠PDK=![]() =tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=
=tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=![]() DK=
DK=![]() (t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(3)如下图3,过点P作PH⊥AD于点H交y轴于点R,由已知条件易证△PHD≌△CNE,从而可得PH=CN,结合CN=OC-ON,PH=t+2可得关于t的方程t+2=t2﹣![]() t+1,解方程可得t1=2,t2=﹣
t+1,解方程可得t1=2,t2=﹣![]() (舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
(舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
试题解析:
(1)∵抛物线y=ax2+bx+6过点A(﹣2,0),B(3,0),则
![]() ,解得:
,解得: ![]() ,
,
故抛物线解析式为y=﹣x2+x+6;
(2)如下图2,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,
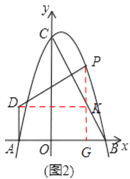
∵PD⊥BC,DE⊥y轴,∠BCO=∠PDK,OB=3,OC=6
∴tan∠BCO=tan∠PDK=![]() ,DK=t+2,PK=
,DK=t+2,PK=![]() DK=
DK=![]() (t+2),
(t+2),
∵DK∥AB,AD⊥AB,
∴四边形ADKG为矩形,
∴AD=KG,
d=AD=KG=PG﹣PK=﹣t2+t+6﹣![]() (t+2)=﹣t2+
(t+2)=﹣t2+![]() t+5(0<t<3);
t+5(0<t<3);
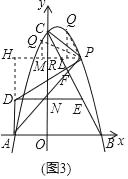
(3)如图3,过点P作PH⊥AD于点H,
在△PHD与△CNE中, 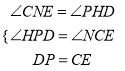 ,
,
∴△PHD≌△CNE,
∴PH=CN=OC﹣ON,
∵四边形ADON为矩形,
∴CN=6﹣(﹣t2+![]() t+5)=t2﹣
t+5)=t2﹣![]() t+1,PH=t+2,
t+1,PH=t+2,
∴t+2=t2﹣![]() t+1,
t+1,
解得t1=2,t2=﹣![]() (舍),
(舍),
把t=2代入抛物线y=﹣x2+x+6=4,
∴点P(2,4),
∵PH与y轴交于点R,PR=CR=2,
∴∠CPR=45°,PH=AH=4,
∴∠APH=45°,
∴∠APC=90°,
∵∠QPC=∠APD,
∴∠QPD=90°,
当点Q在第一象限时,过点Q作QL⊥PH于点L,
∴∠LQP=∠HPD,
∴tan∠LQP=tan∠HPD=![]() ,
,
设点Q(m,﹣m2+m+6),则PL=2﹣m,QL=﹣m2+m+2,则
![]() =
=![]() ,
,
解得m1=1,m2=2(舍),
把m=1 代入﹣m2+m+6=6,
∴Q(1,6),
当点Q在第二象限时,过点Q作QM⊥PH,
∵∠CPH=∠APH=45°∠QPC=∠APD,
∴∠QPM=∠DPH tan∠QPM=tan∠DPH=![]() ,
,
设点Q(n,﹣n2+n+6)PM=2﹣n QM=﹣n2+n+2,
∴![]() =
=![]() ,
,
解得n1=﹣![]() ,n2=2(舍),
,n2=2(舍),
把n=1﹣![]() 代入﹣n2+n+6=
代入﹣n2+n+6=![]() ,
,
∴Q(﹣![]() ,
, ![]() ).
).
综上所述,点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 的中点,
的中点, 是
是 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 ,连接
,连接 .
.
(1)写出四边形
 的形状,并证明:
的形状,并证明:(2)若四边形
 的面积为12,
的面积为12, ,求
,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=80°,∠B=40°.
(1)求作线段BC的垂直平分线DE,垂足为E,交AB于点D;(要求;尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,求证:AC=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B:比较了解C:了解较少,D:不了解”四种,并将调查结果绘制成以下两幅不完整的统计图.
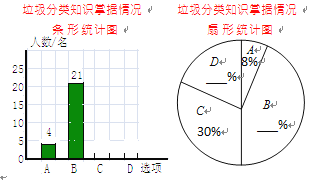
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有________名;
(3)已知“非常了解”的4名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新能源汽车投放市场后,有效改善了城市空气质量。经过市场调查得知,某市去年新能源汽车总量已达到3250辆,预计明年会增长到6370辆.
(1)求今、明两年新能源汽车数量的平均增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
相关试题

