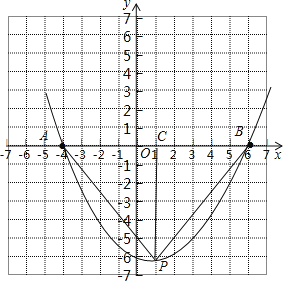
【题目】已知抛物线y=a（x+4）（x﹣6）与x轴交于A，B两点（点A在B的左侧），顶点为P，且点P在直线y=2x+m上．

（1）试用含m的代数式表示a；

（2）若△ABP为直角三角形，试求该抛物线和直线的函数表达式．

参考答案：

【答案】（1）a=﹣；（2）抛物线解析式为y=﹣x2+x+，直线解析式为y=2x+3．

【解析】

试题分析：（1）利用抛物线与x轴的交点问题得到A（﹣4，0），B（6，0），则抛物线的对称轴为直线x=1，所以P点坐标可表示为（1，﹣25a），然后根据一次函数图象上点的坐标特征得到﹣25a=2+m，再用m表示a即可；

（2）根据抛物线的对称性可判断△ABP为等腰直角三角形，作PC⊥x轴于C，如图，根据等腰直角三角形的性质得PC=AB，即|﹣25a|=×（6+4），解得a=±，则可分别计算出对应的m的值，然后写出对应的抛物线解析式和直线解析式．

解：（1）∵抛物线解析式为y=a（x+4）（x﹣6），

∴A（﹣4，0），B（6，0），

∴抛物线的对称轴为直线x=1，

即P点的横坐标为1，

∴P（1，﹣25a），

又∵P在直线y=2x+m上，

∴﹣25a=2+m，

∴a=﹣；

（2）由抛物线的对称性可知，△ABP为等腰直角三角形，且∠APB=90°，

作PC⊥x轴于C，如图，则PC=AB，

∴|﹣25a|=×（6+4），

∴a=±，

当a=时，﹣=，解得m=﹣7，此时抛物线解析式为y=（x+4）（x﹣6），即y=x2﹣x﹣，直线解析式为y=2x﹣7；

当a=﹣时，﹣=﹣，解得m=3，此时抛物线解析式为y=﹣（x+4）（x﹣6），即y=﹣x2+x+，直线解析式为y=2x+3．

关闭