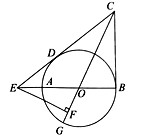
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 分别切⊙
分别切⊙![]() 于点
于点![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() 于点
于点![]() .
.
⑴求证![]() ;
;
⑵若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1);(2).
【解析】
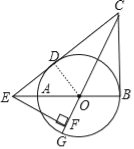
试题分析:(1)利用切线长定理得到OC平分∠BCE,即∠ECO=∠BCO,利用切线的性质得OB⊥BC,则∠BCO+∠COB=90°,由于∠FEB+∠FOE=90°,∠COB=∠FOE,所以∠FEB=∠ECF;
(2)连接OD,如图,利用切线长定理和切线的性质得到CD=CB=6,OD⊥CE,则CE=10,利用勾股定理可计算出BE=8,设⊙O的半径为r,则OD=OB=r,OE=8﹣r,在Rt△ODE中,根据勾股定理得r2+42=(8﹣r)2,解得r=3,所以OE=5,OC=3![]() ,然后证明△OEF∽△OCB,利用相似比可计算出EF的长.
,然后证明△OEF∽△OCB,利用相似比可计算出EF的长.
试题解析(1)证明:∵CB,CD分别切⊙O于点B,D,
∴OC平分∠BCE,即∠ECO=∠BCO,OB⊥BC,∴∠BCO+∠COB=90°,
∵EF⊥OG,∴∠FEB+∠FOE=90°,而∠COB=∠FOE,∴∠FEB=∠ECF;
(2)解:连接OD,如图,
∵CB,CD分别切⊙O于点B,D,∴CD=CB=6,OD⊥CE,∴CE=CD+DE=6+4=10,
在Rt△BCE中,BE=![]() =8,
=8,
设⊙O的半径为r,则OD=OB=r,OE=8﹣r,
在Rt△ODE中,r2+42=(8﹣r)2,解得r=3,
∴OE=8﹣3=5,
在Rt△OBC中,OC=![]() =3
=3![]() ,
,
∵∠COB=∠FOE,∴△OEF∽△OCB,
∴![]() ,即
,即![]() ,∴EF=2
,∴EF=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个容量为16GB的便携式U盘的内存全部用来储数码照片,若每张照片文件大小为211KB,则这个U盘可以存储这样的数码照片张.(16GB=224KB,用2为底的幂表示结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+(3a5b3)÷(a2b)2 , 其中ab=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月29日至10月7日,2019年北京世界园艺博览会在北京延庆举行,园区内率先开展了5G网络的商用试验.已知现在4G网络在理想状态下峰值速率约是100Mbps,而5G网络峰值速率是4G网络的204.8倍,请用科学记数法表示5G网络峰值速率约为______Mbps.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x﹣a﹣5=0的解是x=﹣2,则a的值为( )
A.1
B.﹣1
C.9
D.﹣9 -
科目: 来源: 题型:
查看答案和解析>>【题目】 九⑴班
 名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下
名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下 名学生成绩尚未统计,这
名学生成绩尚未统计,这 名学生成绩如下:
名学生成绩如下: .
.频数分布表
分数段
频数(人数)









请解答下列问题:
⑴完成频数分布表,
 ,
, .
.⑵补全频数分布直方图;
⑶全校共有
 名学生参加初赛,估计该校成绩
名学生参加初赛,估计该校成绩 范围内的学生有多少人?
范围内的学生有多少人?⑷九⑴班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
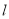 的解析式为
的解析式为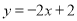 ,分别交
,分别交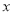 轴、
轴、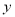 轴于点
轴于点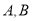 .
.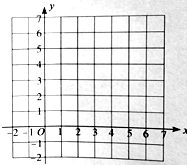
⑴写出
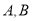 两点的坐标,并画出直线
两点的坐标,并画出直线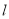 的图象;
的图象;⑵将直线
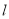 向上平移
向上平移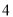 个单位得到
个单位得到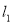 ,
,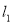 交
交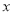 轴于点
轴于点 .作出
.作出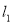 的图象,
的图象,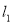 的解析式是 .
的解析式是 .⑶将直线
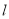 绕点
绕点 顺时针旋转
顺时针旋转 得到
得到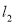 ,
, 交
交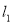 于点
于点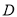 .作出
.作出 的图象,
的图象,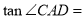 .
.
相关试题

