Question

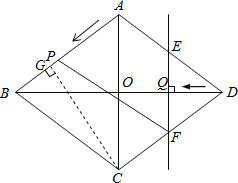
【题目】已知：如图，在菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm．点P从点A出发，沿AB方向匀速运动，速度为1cm/s；过点P作直线PF∥AD，PF交CD于点F，过点F作EF⊥BD，且与AD、BD分别交于点E、Q；连接PE，设点P的运动时间为t（s）（0＜t＜10）．

解答下列问题：

（1）填空：AB= cm；

（2）当t为何值时，PE∥BD；

（3）设四边形APFE的面积为y（cm2）

①求y与t之间的函数关系式；

②若用S表示图形的面积，则是否存在某一时刻t，使得S四边形APFE=S菱形ABCD？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）10；（2）当t=5时，PE∥BD；（3）①，②存在t=4s，使得S四边形APFE=S菱形ABCD．

【解析】

试题分析：（1）由四边形ABCD是菱形，OA=AC，OB=BD．在Rt△AOB中，运用勾股定理求出AB=10．

（2）由△APE∽△ABD，得出，求出t的值即可；

（3）①过点C作CG⊥AB于点G，由S菱形ABCD=ABCG=ACBD，求出CG．据S平行四边形APFD=（AP+DF）CG．S△EFD=EFQD．得出y与t之间的函数关系式；

②由S菱形ABCD=ABCG，求出CG，由S四边形APFE=S菱形ABCD，求出t即可．

解：（1）∵在菱形ABCD中，对角线AC，BD相交于点O，且AC=12cm，BD=16cm，

∴BO=DO=8cm，AO=CO=6cm，

∴AB==10（cm），

故答案为：10；

（2）∵在菱形ABCD中，∴AB∥CD，∠ADB=∠CDB，

又∵PF∥AD，

∴四边形APFD为平行四边形，

∴DF=AP=t，

又∵EF⊥BD于Q，且∠ADB=∠CDB，

∴∠DEF=∠DFE，

∴DE=DF=t，

∴AE=10﹣t，

当PE∥BD时，△APE∽△ABD，

∴，

∴，

∴t=5，

∴当t=5时，PE∥BD；

（3）①∵∠FDQ=∠CDO，∠FQD=∠COD=90°，

∴△DFQ∽△DCO．

∴，

即，

∴．

∴，

同理，，

如图，过点C作CG⊥AB于点G，

∵S菱形ABCD=ABCG=ACBD，

即10CG=×12×16，

∴CG=．

∴S平行四边形APFD=DFCG=，

∴S△EFD=EFQD=

∴，

②当S四边形APFE=S菱形ABCD

则，

即t2﹣20t+64=0，

解这个方程，得t1=4，t2=16＞10（不合，舍去）

∴存在t=4s，使得S四边形APFE=S菱形ABCD．