【题目】如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-1,3),B(-4,0),C(0,0)
(1)①画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;②画出将△ABC绕原点O顺时针方向旋转90°得到的△A2B2O;
(2)在x轴上存在一点P,满足点P到点A1与点A2的距离之和最小,请直接写出P点的坐标.
参考答案:
【答案】
(1)解:如图,△A1B1C1、△A2B2O为所求作的三角形.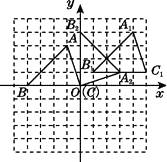
(2)解:如图,作点A1关于x轴的对称点A3 , 连接A2A3 , 交x轴于点P,即P为所求作的点。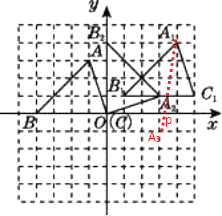
∵A1地坐标为(3,1),A3(4,4)
∴A3的坐标为(3,-1)
设直线A2A3的解析式为y=kx+b![]()
解之:![]()
∴直线A2A3的解析式为y=5x-16.
当y=0时,5x-16=0
解之:x=![]()
故P点的坐标为 ![]() .
.
【解析】(1)分别将点A、B、C向上平移1个单位,再向右平移5个单位,然后顺次连接即可;根据网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点,然后顺次连接即可。
(2)利用最短路径问题解决,首先作A1点关于x轴的对称点A3 , 再连接A2A3与x轴的交点就是点P,再求出直线A2A3的解析式,然后求出直线A2A3与x轴的交点坐标即为所求的点P的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣2,4)位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果t是方程x2﹣2x﹣1=0的根,那么代数式2t2﹣4t的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根是2﹣m和3m+6,则m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.

(1)求证:△COD是等边三角形.
(2)当α=150°时,试判断△AOD的形状.
(3)探究:当α为多少度时,△AOD是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x,y),且|x﹣2|+|y+4|=0,则点P在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到
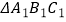 ,再作
,再作 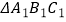 关于x轴对称的图形
关于x轴对称的图形  ,则顶点
,则顶点 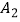 的坐标是( )
的坐标是( )
A.(-3,-2)
B.(2,-3)
C.(-2,3)
D.(-2,-3)
相关试题

