搜索
【题目】如图，在平面直角坐标系xOy中，一次函数y＝﹣x的图象与反比例函数y＝
（x＜0）的图象相交于点A（﹣4，m）．
（1）求反比例函数y＝的解析式；
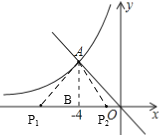
（2）若点P在x轴上，AP＝5，直接写出点P的坐标．
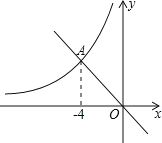
参考答案：
【答案】（1）y＝﹣
；（2）P点的坐标是（﹣7，0）或（﹣1，0）．
【解析】
(1)先求出A的坐标，再代入反比例函数解析式求出即可；
(2)根据勾股定理求出即可．
(1)∵A(﹣4，m)在一次函数y＝﹣x上，
∴m＝4，
即A(﹣4，4)，
∵A在反比例函数y＝
(x＜0)的图象上，
∴k＝﹣16，
∴反比例函数y＝的解析式是y＝﹣；
(2)∵Rt△ABP中，∠ABP=90°，AB=4，AP=5，
∴BP=
=3，
-4-3=-7，-4+3=-1，
∴P点的坐标是(﹣7，0)或(﹣1，0)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学将组织七年级学生春游一天，由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜．
（1）两同学向公司经理了解租车的价格，公司经理对他们说：“公司有45座和60座两种型号的客车可供租用，60座的客车每辆每天的租金比45座的贵100元．”王老师说：“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车，一天的租金为1600元，你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下，都说知道了价格．
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗？
（2）公司经理问：“你们准备怎样租车”，甲同学说：“我的方案是只租用45座的客车，可是会有一辆客车空出30个座位”；乙同学说“我的方案只租用60座客车，正好坐满且比甲同学的方案少用两辆客车”，王老师在﹣旁听了他们的谈话说：“从经济角度考虑，还有别的方案吗”？如果是你，你该如何设计租车方案，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的不等式
＞
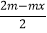x﹣1．（1）当m=1时，求该不等式的解集；
（2）m取何值时，该不等式有解，并求出解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起．
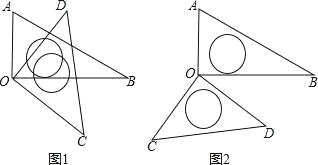
（ 1 ） 如图 1 ， 若∠ BOD=35° ， 则∠ AOC= ； 若∠AOC=135°， 则∠BOD= ；
（2）如图2，若∠AOC=140°，则∠BOD= ；
（3）猜想∠AOC 与∠BOD 的大小关系，并结合图1说明理由．
（4）三角尺 AOB 不动，将三角尺 COD 的 OD 边与 OA 边重合，然后绕点 O 按顺时针或逆时针方向任意转动一个角度，当∠A OD（0°＜∠AOD＜90°）等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠AOD 角度所有可能的值，不用说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F，切点为G，连接AG交CD于K．
（1）如图1，求证：KE=GE；
（2）如图2，连接CABG，若∠FGB=
∠ACH，求证：CA∥FE；（3）如图3，在（2）的条件下，连接CG交AB于点N，若sinE=
，AK=
，求CN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣
），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有一工程需在规定日期x天内完成，如果甲单独工作刚好能够按期完成：如果乙单独工作就要超过规定日期3天．
（1）甲的工作效率为 ，乙的工作效率为 ．（用含x的代数式表示）
（2）若甲、乙合作2天后余下的工程由乙单独完成刚好在规定日期完成，求x的值．
相关试题
