【题目】以下是两张不同类型火车的车票(“![]() 次”表示动车,“
次”表示动车,“![]() 次”表示高铁):
次”表示高铁):

(1)根据车票中的信息填空:该列动车和高铁是__________向而行(填“相”或“同”).
(2)已知该列动车和高铁的平均速度分别为![]() 、
、![]() ,两列火车的长度不计.
,两列火车的长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到![]() ,求
,求![]() 、
、![]() 两地之间的距离.
两地之间的距离.
②在①中测算的数据基础上,已知![]() 、
、![]() 两地途中依次设有
两地途中依次设有![]() 个站点
个站点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,动车每个站点都停靠,高铁只停靠
,动车每个站点都停靠,高铁只停靠![]() 、
、![]() 两个站点,两列火车在每个停靠站点都停留
两个站点,两列火车在每个停靠站点都停留![]() .求该列高铁追上动车的时刻.
.求该列高铁追上动车的时刻.
参考答案:
【答案】(1)同;(2)①1200km,②8点55分.
【解析】试题分析:(1)由车票可以得出动车和高铁都是由A地开往B地,所以动车和高铁是同向而行;(2)高铁比动车晚出发1个小时,所以动车比高铁全程多花了2个小时,设A、B两地距离为xkm,则可列方程![]() -
-![]() =2,解出x即可;(3)每个相邻站点距离为:1200÷6=200km,
=2,解出x即可;(3)每个相邻站点距离为:1200÷6=200km,
高铁到每站所花时间为:200÷300=![]() h=40min,动车到每站所花时间为:200÷200=1h=60min,
h=40min,动车到每站所花时间为:200÷200=1h=60min,
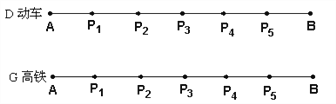
画出动车和高铁到每一站的时间图,由此可以得出高铁在P2、P3之间追上并超过动车,设高铁经过y小时后追上动车,则(y-![]() )×300=(y+1-
)×300=(y+1-![]() ×2)×200,解得y=
×2)×200,解得y=![]() .
.
所以高铁在经过![]() h后可以追上动车,追上的时刻为8点55分.
h后可以追上动车,追上的时刻为8点55分.
试题解析:
(1)同;
(2)①设A、B两地距离为xkm,则
![]() -
-![]() =2,解得x=1200,
=2,解得x=1200,
所以A、B两地之间的距离为1200km;
②每个相邻站点距离为:1200÷6=200km,
高铁到每站所花时间为:200÷300=![]() h=40min,动车到每站所花时间为:200÷200=1h=60min,
h=40min,动车到每站所花时间为:200÷200=1h=60min,
所以动车和高铁到每一站的时间如图所示:

由此可以得出高铁在P2、P3之间追上并超过动车,
设高铁经过y小时后追上动车,
则(y-![]() )×300=(y+1-
)×300=(y+1-![]() ×2)×200,解得y=
×2)×200,解得y=![]() .
.
所以高铁在经过![]() h后可以追上动车,追上的时刻为8点55分.
h后可以追上动车,追上的时刻为8点55分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
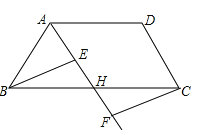
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是 ,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:5x2+4﹣3x2﹣5x﹣2x2﹣5+6x,其中x=﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(-1,2)向右平移3个单位长度,再向下平移5个单位长度,则平移后点的坐标是( )
A.(2,3)B.(-2,-3)C.(2,-3)D.(-2,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题
(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①“随意翻到一本书的某页,这页的页码一定是奇数”;②“明天太阳从东方升起”( )
A.只有①正确B.只有②正确C.①②都正确D.①②都错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】只用下列正多边形,不能进行平面镶嵌的是( )
A.正方形B.等边三角形C.正六边形D.正十一边形
相关试题

