【题目】如图所示,在折线ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延长AB,GF交于点M.试探索∠AMG与∠3的关系,并说明理由. 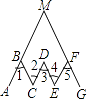
参考答案:
【答案】解:∠AMG=∠3.理由如下: ∵∠2=∠3,
∴BC∥DE,
∵∠4=∠5,
∴DE∥FG,
∴BC∥FG,
∴∠1=∠AMG,
而∠1=∠3,
∴∠AMG=∠3.
【解析】根据平行线的判定由∠2=∠3得到BC∥DE,由∠4=∠5得到DE∥FG,则BC∥FG,根据平行线的性质得∠1=∠AMG,∠1=∠3,则∠AMG=∠3.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式6m3﹣2m2+4m+2减去3(2m3+m2+3m﹣1),再减去3(2m3+m2+3m﹣1)(m为整数)的差一定是( )
A.5的倍数
B.偶数
C.3的倍数
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表(图1)和频数分布直方图(图2).

请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= (2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是 ;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】青山村种的水稻2010年平均每公顷产7200kg,2012年平均每公顷产8450kg,求水稻每公顷产量的年平均增长率,设水稻每公顷产量的年平均增长率为x,则所列方程正确的为( )
A.7200(1+x)=8450
B.7200(1+x)2=8450
C.7200+x2=8450
D.8450(1﹣x)2=7200 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ADE∽△ABC,相似比为2:3,则S△ADE:S△ABC的值为_____.
-
科目: 来源: 题型:
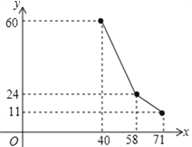
查看答案和解析>>【题目】国家为支持大学生创业,提供小额无息贷款,学生王芳享受政策无息贷款36000元用来代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人每天82元,每天应支付其它费用106元.
(1)求日销售y(件)与销售价x (元/件)之间的函数关系式;
(2)若暂不考虑还贷,当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则该店至少需要多少天才能还清贷款,此时,每件服装的价格应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某天的最高气温为﹣2℃,最低气温为﹣8℃,这天的温差是℃.
相关试题

