【题目】如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,到达A点停止运动;同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,到达D点停止运动,设点E移动的时间为t(秒).
(1)当t=1时,求四边形BCFE的面积;
(2)设四边形BCFE的面积为S,求S与t之间的关系式,并写出t的取值范围;
(3)若F点到达D点后立即返回,并在线段CD上往返运动,当E点到达A点时它们同时停止运动,求当t为何值时,以E,F,D三点为顶点的三角形是等腰三角形,并求出此的等腰三角形的面积S△EDF.

参考答案:
【答案】(1)S四边形BCFE=17;(2)S=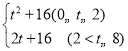 ;(3)当t=
;(3)当t=![]() 时,S△DEF=
时,S△DEF=![]() .当t=4时,S△DEF=8.
.当t=4时,S△DEF=8.
【解析】
(1)如图1中,t=1时,DE=1,CF=2,根据S四边形BCFE=S△BCE+S△ECF计算即可.
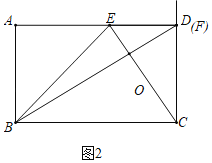
(2)分两种情形:如图1中,当0≤t≤2时,如图2中,当2<t≤8时,分别求解即可解决问题.
(3)由题意当DE=DF时,△DEF是等腰直角三角形.分两种情形分别构建方程解决问题即可.
解:(1)如图1中,
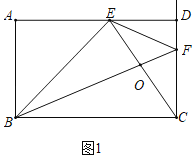
t=1时,DE=1,CF=2,
∴S四边形BCFE=S△BCE+S△ECF=![]() ×8×4+
×8×4+![]() ×2×1=17.
×2×1=17.
(2)如图1中,当0≤t≤2时,S=S△BCE+S△ECF=![]() ×8×4+
×8×4+![]() ×2t×t=t2+16.
×2t×t=t2+16.
如图2中,当2<t≤8时,S=S△BCE+S△EDC=![]() ×8×4+
×8×4+![]() ×4×t=2t+16.
×4×t=2t+16.
综上所述,S=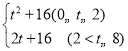 .
.
(3)由题意当DE=DF时,△DEF是等腰直角三角形.
可得4﹣2t=t或2t﹣4=t,
解得t=![]() 或4.
或4.
当t=![]() 时,S△DEF=
时,S△DEF=![]() ×
×![]() ×
×![]() =
=![]() .
.
当t=4时,S△DEF=![]() ×4×4=8.
×4×4=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程
 x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.现在把上面的题目改编为下面的两个小题,请解答.
x2-x=2化为一元二次方程的一般形式,并写出它的二次项系数、一次项系数和常数项.现在把上面的题目改编为下面的两个小题,请解答.(1)下列式子中,有哪几个是方程
 x2-x=2所化的一元二次方程的一般形式?(答案只写序号)
x2-x=2所化的一元二次方程的一般形式?(答案只写序号)①
 x2-x-2=0;②-
x2-x-2=0;②- x2+x+2=0;③x2-2x-4=0;
x2+x+2=0;③x2-2x-4=0;④-x2+2x+4=0; ⑤
 x2-2
x2-2 x-4
x-4 =0.
=0.(2)方程
 x2-x=2化为一元二次方程的一般形式,它的二次项系数,一次项系数,常数项之间具有什么关系?
x2-x=2化为一元二次方程的一般形式,它的二次项系数,一次项系数,常数项之间具有什么关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料,再解答下列问题:
题:分解因式:
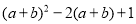
解:将“
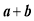 ”看成整体,设
”看成整体,设 ,则原式=
,则原式=

再将“
 ”还原,得原式=
”还原,得原式=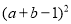 .
.上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:
 ;
; .
.(2)因式分解:
 ;
; .
.(3)求证:若
 为正整数,则式子
为正整数,则式子 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A.
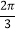 B. 2
B. 2 -
- C. 2
C. 2 -
-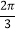 D. 4
D. 4 -
-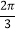
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
,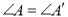 ,若
,若 ,则还需添加的一个条件有( )
,则还需添加的一个条件有( )

A.
 种B.
种B. 种C.
种C. 种D.
种D. 种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】黑板上写有1,
 ,
, ,
, ,…,
,…, 共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____.
共100个数字,每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+1,则经过_____次操作后,黑板上只剩下一个数,这个数是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.
(1)求∠AOB的度数:
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数
(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE= .

相关试题

