【题目】某校为了推进学校均衡发展,计划再购进一批图书,丰富学生的课外阅读.为了解学生对课外阅读的需求情况,学校对学生所喜爱的读物:A.文学,B.艺术,C.科普,D.生活,E.其他,进行了随机抽样调查(规定每名学生只能选其中一类读物),并将调查结果绘制成以下不完整的统计图表.

(1)a= ,b= ,请补全条形统计图;
(2)如果全校有2500名学生,请你估计全校有多少名学生喜爱科普读物;
(3)学校从喜爱科普读物的学生中选拔出2名男生和3名女生,并从中随机抽取2名学生参加科普知识竞赛,请你用树状图或列表法求出恰好抽到一名男生和一名女生的概率.
参考答案:
【答案】(1)80,64;(2)750;(3)![]() .
.
【解析】试题分析:(1)由E类型的人数及其百分比求得总人数,总人数乘以A类型百分比可得其人数,在用总人数减去其余各组人数得出D类型人数,即可补全条形图;
(2)用总人数乘以样本中C类型所占比例即可得;
(3)用列表法或画树状图法列出所有等可能结果,从中确定恰好抽到一名男生和一名女生的结果数,根据概率公式求解可得.
试题解析:解:(1)∵抽查的总人数为:32÷10%=320人,∴a=320×25%=80人,b=320﹣80﹣48﹣96﹣32=64人;
补全条形统计图如下:
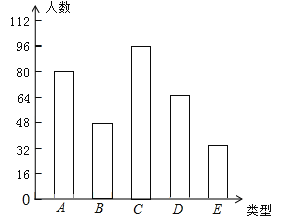
故答案为:80,64;
(2)2500×![]() =750人.
=750人.
答:估计全校喜爱科普读物的学生约有750人.
(3)列表得:

或画树状图得:

所有等可能的情况数有20种,其中一男一女的有12种,所以P(恰好抽到一男一女)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2(a﹣4)+(4﹣a)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3(__________________________)
又∵HG∥CD(已知)
∴∠2=∠4(_______________________________)
∵AB∥CD(已知)
∴∠BEF+___________=180°(_____________________)
又∵EG平分∠BEF,FG平分∠EFD (已知)
∴∠1=(______)∠BEF,∠2=(______)∠EFD (______________________)
∴∠1+∠2=(________) (∠BEF +∠EFD)=(____________)
∴∠3+∠4=90°(_______________________)即∠EGF=90°

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 (a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.
(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=2,OB=8,OC=6.(1)求抛物线的解析式;
(2)点M从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时,点N从B出发,在线段BC上以每秒1个单位长度的速度向C点运动,当其中一个点到达终点时,另一个点也停止运动,当△MBN存在时,求运动多少秒使△MBN的面积最大,最大面积是多少?
(3)在(2)的条件下,△MBN面积最大时,在BC上方的抛物线上是否存在点P,使△BPC的面积是△MBN面积的9倍?若存在,求点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将0.09493用四舍五入法取近似值精确到百分位,其结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地海拔高度分别为20米和﹣9米,那么甲地比乙地高_____米.
-
科目: 来源: 题型:
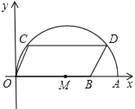
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
相关试题

